En el capítulo anterior vimos que el álgebra Boleana es un arma poderosa para el estudio de los circuitos lógicos.
Sin embargo, el álgebra Boleana tiene sus limitaciones.
Considérese la siguiente expresión:
AB + B
Aparentemente, esta expresión ya no se puede simplificar. Sin embargo, podemos comprobar (construyendo las Tablas de Verdad) que esta expresión cuya simplificación no es tan obvia pese a todo es equivalente a la siguiente expresión:
A + B
la cual es mucho más sencilla. Se hace evidente que hay casos en los cuales el álgebra Boleana no es suficiente. Tenemos pues que recurrir a otras técnicas que la complementen.
Los diagramas de subconjuntos nos proporcionan una manera sencilla de poder visualizar las relaciones que puede haber entre varias variables. Quizá los diagramas más sencillos de todos son los que representan al "1" lógico, el cual podemos representar como un cuadro completamente lleno, y al "0" lógico, el cual podemos representar como un cuadro completamente vacío:
En este tipo de diagramas, no sólo podemos representar el "uno" y el "cero". También podemos representar variables. El diagrama más sencillo de todos es el que utilizamos para representar una sola variable, el cual está dividido en dos partes: una parte "llena" que es la parte en la cual la variable A toma el valor de "1" (a la izquierda, de color ciano), y la parte "vacía" que es la parte en la cual la variable A toma el valor de "0" (a la derecha, sin color):
Pero con estos diagramas no sólo podemos representar a la variable. También podemos representar el inverso lógico de la variable, el cual será como se muestra a continuación:
Del mismo modo, podemos representar una segunda variable B y el complemento de la misma de la siguiente manera:
Superimponiendo ambas variables en un mismo diagrama, podemos contestar algunas preguntas interesantes como la siguiente: ¿en qué parte del diagrama mixto se encontrará la región en la cual ambas variables A y B se traslapan? La respuesta se dá a continuación:
A continuación tenemos la región en donde la variable A se traslapa con el complemento de la variable B, así como la región en la cual los complementos de ambas variables se traslapan:
Hagámonos ahora otra pregunta: ¿cuál sería la región en la cual las variables A y B se unen (en lugar de intersectarse), la porción del diagrama en donde podemos estar ya sea en A ó en B, o sea la región que representaría la suma Boleana A+B de dichas variables? La respuesta se dá a continuación:
Y el área que representa la suma Boleana de los complementos de ambas variables es la siguiente:
Por su parte, la expresión Boleana AB+AB que representa la salida de un bloque OR-EXCLUSIVO es la siguiente:
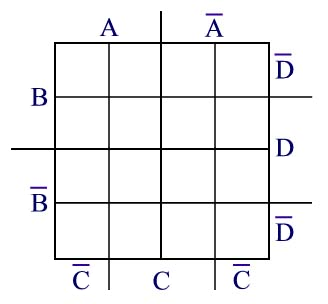
Si queremos superimponer en el mismo mapa una tercera variable C, lo podemos hacer de la siguiente manera:
Y si queremos superimponer en el mismo mapa una cuarta variable D, lo podemos hacer de la siguiente manera:
El mismo procedimiento constructivo se puede extender hacia una quinta variable e inclusive hacia una sexta variable, aunque la ventaja de visualización se va perdiendo rápidamente encima de las cuatro variables.
Para representar en el mapa una expresión elaborada como (A+B)(C+D):
primero localizamos en el mapa la región que representa la suma de las regiones A y B, o lo que es lo mismo, la suma Boleana de las variables A y B:
tras lo cual localizamos en el mapa la región que representa la suma de las regiones C y D, o lo que es lo mismo, la suma Boleana de las variables C y D:
tras lo cual obtenemos un mapa que represente las regiones que ambos mapas de A+B y C+D tengan en común, o sea la región común en la que ambos se intersectan, lo cual equivale a llevar a cabo la operación lógica AND de A+B y de C+D.
Los diagramas de subconjuntos permiten verificar de manera casi inmediata todos los teoremas Boleanos que fueron demostrados en el capítulo anterior. Por ejemplo, el teorema que dice:
A + A = 1
es verificado de la siguiente manera:
Es importante señalar que para los matemáticos puros, esto no constituye una demostración formal, sino una simple verificación de un teorema. Sin embargo, entanto que nosotros mismos nos podamos convencer visualmente de la veracidad de algún enunciado Boleano mediante este recurso, podemos hacer a un lado el rigorismo formalista y continuar adelante con la mentalidad típica del ingeniero que busca procedimientos que den resultados comprobados en la práctica.
Con cambios mínimos, los diagramas de subconjuntos nos sirven de base para introducirnos a una de las herramientas de simplificación de circuitos lógicos más populares que hay. Estudiaremos a continuación el siguiente mapa para dos variables boleanas A y B conocido como el mapa de Karnaugh, inventado en 1952 por Edward W. Veitch y refinado posteriormente por Maurice Karnaugh, un ingeniero de telecomunicaciones trabajando para Bell Labs:
Para la construcción de nuestro primer mapa de Karnaugh, utilizaremos un concepto introducido en la sección de problemas resueltos del capítulo anterior, el concepto del minterm. Supóngase que desamos localizar el minterm AB en el mapa de Karnaugh. Estudiando el mapa detenidamente, vemos que podemos representar dicho minterm en el mapa como se muestra a continuación:
De la misma manera, si deseamos representar los minterms AB y A·B en el mapa de Karnaugh, podemos hacerlo de la siguiente manera:
Ahora bien, también podemos representar variables sencillas en el mapa de Karnaugh. Supóngase que deseamos representar B en el mapa de Karnaugh. Esto lo logramos de la siguiente manera:
Estudiamos ahora un hecho de importancia trascendental. Este último mapa de Karnaugh nos indica que B es igual a la suma de los minterms AB y A·B, lo cual podemos comprobar mediante el álgebra Boleana como sigue:
AB + A·B = (A + A)B = (1)B = B
Tenemos aquí nuestra primera indicación sobre cómo podemos usar el mapa de Karnaugh para simplificar circuitos lógicos.
Supóngase que la salida de un circuito está dada por la siguiente expresión:
Salida = AB + A·B
Podemos describir la salida del circuito en un mapa de Karnaugh de la manera siguiente:
Vemos de inmediato en el mapa cómo los minterms AB y A·B forman dos grupos adyacentes que están cubiertos completamente en el mapa por la variable A. Concluímos, pues, que la salida simplificada del circuito está dada por la siguiente expresión:
Salida = A
La regla general para simplificar un circuito usando el mapa de Karnaugh es examinar el mapa que le corresponde y determinar los agrupamientos más grandes de grupos adyacentes que se pueden describir con el menor número de variables boleanas.
Usando el mapa de Karnaugh, tratemos ahora de simplificar la expresión que encontramos al comienzo de este capítulo:
AB + B
Su mapa de Karnaugh con una simplificación posible tendrá el siguiente aspecto (el "minterm" correspondiente a la variable B está enmarcado dentro de una línea verde cubriendo todo el renglón representativo de B, mientras que el "minterm" AB es puesto antes de los agrupamientos simplificadores en la esquina inferior izquierda) :
Como se puede ver, es posible hacer dos agrupamientos de grupos adyacentes, los cuales están descritos por la expresión:
A + B
que es la expresión simplificada que buscábamos.
Asimismo, el mapa de Karnaugh nos indica cuáles son las expresiones que no se pueden simplificar. Por ejemplo, la siguiente expresión:
AB + AB
está descrita por el siguiente mapa:
Esta expresión, como se puede ver en su mapa de Karnaugh, ya no se puede simplificar.
Existen también mapas de Karnaugh para expresiones con tres o más variables, algunos de los cuales se muestran al final de esta introducción.
Supóngase que deseamos simplificar un circuito con tres variables de entrada A, B y C cuya salida es la siguiente:
ABC + A·B·C + ABC + + A·B·C
En este caso, tenemos que utilizar el mapa de Karnaugh para tres variables:
El mapa de Karnaugh para la expresión lógica dada se muestra a continuación:
La primera simplificación es evidente. Los minterms ABC y ABC pueden ser agrupados para ser representados por la relación BC (esta agrupación es la que corresponde a los unos que están encerrados dentro del rectángulo rojo). La siguiente simplificación no es tan obvia.
Obsérvese que si conectamos los vértices del mapa alrededor de un cilindro (esto es, si enrollamos el mapa y unimos el lado izquierdo con el lado derecho), se puede llevar a cabo otra simplificación. En efecto, los minterms A·B·C y A·B·C se pueden agrupar dentro de la relación BC (correspondiente a los unos que están encerrados dentro del rectángulo verde).
La salida simplificada será por lo tanto:
BC + B·C
Consideremos un circuito cuya Tabla de Verdad es la siguiente:
Podemos representar esta expresión de salida en función no de sus minterms sino de sus maxterms, los cuales fueron introducidos en la sección de problemas resueltos del capítulo anterior, basados en el producto-de-sumas en lugar de la suma-de-productos, como se muestra en el siguiente mapa de Karnaugh:
Como se muestra en el mapa, los maxtems A+B y A+B se pueden agrupar dentro del "maxterm" B.
Asimismo, los maxterms A+B y A+B se pueden agrupar para formar el "maxterm" A.
Puesto que la salida del circuito sigue siendo el producto de sus maxterms, la salida en este caso será:
Salida = (A)(B) = AB
Este es el resultado que buscábamos.
El mapa de Karnaugh se puede extender para manejar cuatro variables, como se muestra a continuación:
Para intentar simplificar un circuito lógico con cinco variables, podemos recurrir a un mapa de Karnaugh como el siguiente:
Existe otro tipo de representación para el mapa de Karnaugh, la cual es completamente equivalente a la que ya hemos visto. Bajo esta representación, a continuación tenemos un mapa de Karnaugh para dos variables A y B:
Aquí la entrada correspondiente a la combinación AB=01 estará situada en el segundo renglón y en la primera columna. Esta representación es completamente a la representación que vimos al principio. A continuación se muestran los dos tipos de representación, lado a lado, para dos variables A y B:
Para tres variables de entrada A, B y C, bajo la representación alterna un mapa de Karnaugh tendrá el siguiente aspecto:
Aquí el casillero correspondiente a la entrada ABC= 011 estará situado en el segundo renglón y en la segunda columna. Y el casillero correspondiente a la entrada ABC=101 estará situado en el primer renglón y en la cuarta columna.
Y para cuatro variables A, B, C y D, el mapa de Karnaugh para este tipo de representación será el siguiente:
El acomodo de variables en el mapa se puede llevar a cabo de acuerdo con las preferencias personales de cada persona, lo principal es que en el mapa aparezcan de modo apropiado todas las variables con todos sus diversos valores posibles de "unos" y "ceros".
A continuación se llevará a cabo la simplificación de un circuito lógico de tres variables a, b y c, mediante un mapa de Karnaugh de este tipo trazado de la siguiente manera:
Dentro de este mapa de Karnaugh, se destacarán las combinaciones de valores tanto de las entradas como de la salida:
El propósito del mapa de Karnaugh es aprovechar al máximo la capacidad humana de poder "agrupar" visualmente patrones similares para poder descubrir así los agrupamientos de "unos" (o alternamente, de "ceros") que pueden resultar en una simplificación. En este caso, podemos llevar a cabo los siguientes agrupamientos:
El siguiente esquema nos muestra agrupados todos los pasos agrupados para llevar a cabo la simplificación de un circuito lógico con dos variables de entrada con este tipo de mapa de Karnaugh:
Empezamos con el circuito lógico puesto en la esquina inferior izquierda, obteniendo del mismo la expresión de su salida lógica Out puesta en la esquina superior izquierda:
Out = AB + AB + AB
Esta expresión está justo en la forma que requerimos (suma-de-productos) para construír el mapa de Karnaugh usando minterms. El término AB nos produce un "1" cuando A=0 y B=1, y esta es nuestra primera entrada en el mapa de Karnaugh. El término AB nos produce un "1" cuando A=1 y B=0, y esta es nuestra segunda entrada en el mapa de Karnaugh. Y por último, el término AB nos produce un "1" cuando A=1 y B=1, y esta es nuestra tercera entrada en el mapa de Karnaugh.
El siguiente paso consiste en llevar a cabo los agrupamientos que nos pueden dar una simplificación del circuito. Estos son mostrados en el mapa de Karnaugh puesto en la esquina superior derecha. El primer agrupamiento como "minterm" más sencillo es la variable A (agrupando los valores de A=1) y el segundo agrupamiento como "minterm" más sencillo es la variable B (agrupando los valores de B=1). Los "minterms" simplificados en el mapa de Karnaugh nos dicen que podemos reemplazar la expresión original por la siguiente expresión (en suma-de-produtos) más simplificada:
Out = A + B
El circuito lógico simplificado se muestra en la esquina inferior derecha del diagrama, el cual requiere un solo componente lógico, un OR, a diferencia del circuito original que requería de cuatro componentes, tres AND y un OR.
Considérese ahora un circuito lógico cuya salida Out está dada por la siguiente expresión:
Out = A·B·C + AB·C + ABC + AB + ABC
Este circuito lógico con tres variables de entrada tiene una salida dada como suma de productos, lo cual nos permite localizar los "1" de los minterms que van dentro del mapa de Karnaugh y lo cual nos permite llevar a cabo la simplificación "enrollando" el mapa alrededor de un cilindro como se muestra:
No resulta difícil ver que la versión simplificada es simplemente:
Out = C
A continuación tenemos otro mapa de Karnaugh, ahora para un circuito con cuatro variables de entrada A, B, C y D, tanto antes como después de haber encontrado un conjunto de posibles simplificaciones:
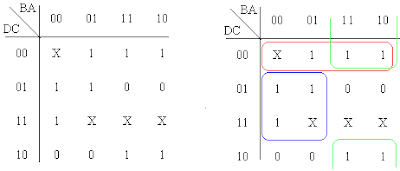
Existen muchos casos en los cuales no todas las combinaciones lógicas de "ceros" y "unos" a la entrada de un circuito son necesarias; un ejemplo de ello es el de un decodificador que toma un número binario de cuatro bits a su entrada y lo convierte en una combinación de siete salidas para encender selectivamente los segmentos de un indicador luminoso numérico hecho a base de diodos emisores de luz LED; en este caso no se utilizará ninguna de las combinaciones entre "1010" y "1111" puesto que no representan dígito alguno en el sistema numérico decimal. Cuando tenemos algunas condiciones dentro de un circuito lógico en las cuales la salida puede ser ya sea un "0" ó un "1" sin consecuencia alguna para el diseño final (conocidas en la literatura de habla inglesa como condiciones don't care), podemos representar dichas condiciones simplemente con una "X" que se sobreentiende que puede tener un valor de "0" ó de "1". A continuación tenemos otro mapa de Karnaugh para un circuito con cuatro variables de entrada A, B, C, D, y cuatro condiciones "X", tanto antes como después de haber encontrado para dicho circuito un conjunto de posibles simplificaciones:
Como puede verse en una de las simplificaciones, la simplificación encerrada bajo una línea de color rojo, estamos aprovechando la ventaja de que "X" puede representar ya sea un "0" ó un "1" para tomarlo como un "1" y juntarlo con los demás "unos" del agrupamiento. Esto mismo se ha llevado a cabo en la simplificación encerrada bajo una línea de color azul en donde también hemos agrupado "unos".
Por lo general, para un circuito lógico con más de cuatro variables de entrada el uso del mapa de Karnaugh va perdiendo su ventaja visual como instrumento de simplificación. Para un circuito lógico con más de cinco o seis variables de entrada, se recomienda el uso de otro método o inclusive de alguno de varios programas computacionales especializados para lograr minimizar un circuito lógico a su expresión más sencilla, muchos de los cuales están basados en otro método de simplificación de circuitos lógicos que va de la mano con el mapa de Karnaugh, el método de Quine-McCluskey, del cual se dará a continuación una introducción.
El estudio del método de Quine-McCluskey nos lleva a definir de manera más formal cierta terminología que hemos pasado por alto, empezando con la definición de los implicantes primarios (prime implicants). En primer lugar, para una salida Y, un implicante se define como un producto normal de dos o más variables (normal en el sentido de que cada variable en el producto aparece una sola vez, con lo cual se descalifica a expresiones como AAB o ABBC) que implica a Y (esto es, produce un "1" en la columna correspondiente a la salida del circuito en su Tabla de Verdad), como en la expresión:
Y = AB + ABC + BC
en donde los implicantes son AB, ABC y BC porque cualquiera de ellos implica a Y. Definido esto, definimos a continuación a un implicante primario como un implicante de Y tal que si cualquiera de sus variables es removida, el término que nos queda ya no implica a Y. Esto quiere decir que en la expresión anterior AB y BC son implicantes primarios (no es posible remover ninguna de las variables en ellos sin que pierdan su relevancia), mientras que ABC no es un implicante primario ya que si se le remueve la variable A esto nos deja con el término BC que sigue implicando a Y porque dicho término está contenido en la expresión original de Y. El hecho de que un implicante no sea un implicante primario tiene que ver directamente con una simplificación Boleana como la siguiente:
A∙B·C∙D + ABC = A∙B·C(D + 1) = A∙B·C
en la cual el implicante primario ABC se "come" al implicante A∙B·C∙D que contiene la variable D que podemos considerar superflua. Cabe notar que un implicante primario no puede ser reducido más, ya que no contiene ninguna variable que pueda ser "comida" al combinarlo con cualquiera de los otros términos en una expresión Boleana; precisamente por ello es un implicante primario. Es de notar que el método de simplificación de Quine-McCluskey es conocido también como el método de implicantes primarios, siendo funcionalmente idéntico al mapa de Karnaugh pero con una forma tabular que hace más accesible su implementación en programas de computadora (el mapa de Karnaugh por ser un método visual no se presta a la elaboración de un programa de computadora que busque el diseño óptimo sin intervención humana), y el cual es superior al mapa de Karnaugh en el sentido de que siempre garantiza la obtención del diseño más económico posible.
Al cubrir el tema del método de Quine-McCluskey, es rutinario en los libros de texto utilizar una notación en la cual a los minterms se les designa de acuerdo con el valor numérico binario que poseen en su notación de "unos" y "ceros". Esta notación proporciona una manera compacta de listar los minterms de una expresión Boleana, lo cual nos puede resultar conveniente en expresiones con más de cuatro variables. Bajo la notación compacta, en una función Boleana de tres variables el minterm ABC proveniente de la combinación binaria "111" es representado precisamente con dicha combinación binaria, simplificada a su equivalente decimal que es 7, mientras que el minterm A·B·C proveniente de la combinación "000" es representado por el decimal 0. Del mismo modo, un minterm como ABC es representado por "011" o bien por el decimal 3. Esto permite representar una expresión Boleana como:
f(A,B,C,D) = ABC + AB·C + A·BC
como la suma de los minterms cuyos equivalentes decimales son 011 (3), 100 (4) y 001 (1), o más elegantemente usando la letra griega sigma mayúscula (Σ) que indica una sumación de términos:
f(A,B,C,D) = Σm(001,011,100)
f(A,B,C,D)= Σm(1,3,4)
f(A,B,C,D)= Σm(1,3,4)
en donde "Σm" se lee como "la suma de minterms"
Del mismo modo, para la siguiente función de tres variables:
Z = f(A,B,C,D) = A·B·C + A·BC + AB·C + ABC
Z = Σm(000,001,100,101)
Z = Σm(0,1,4,5)
Z = Σm(000,001,100,101)
Z = Σm(0,1,4,5)
así como para la siguiente función de cuatro variables:
f(A,B,C,D) = A·B·C·D + A·B·CD + A·BCD + A·BCD + ABCD + ABCD + AB·C·D
+ ABCD + ABC·D + ABCD + ABCD
+ ABCD + ABC·D + ABCD + ABCD
f(A,B,C,D) = Σm(0000,0001,0010,0011,0101,0111,1000,1010,1100,1101,1111)
f(A, B, C, D) = Σm(0,1,2,3,5,7,8,10,12,13,15)
f(A, B, C, D) = Σm(0,1,2,3,5,7,8,10,12,13,15)
Si algún término contiene menos variables que el número total de variables especificado por la Tabla de Verdad, cada variable "ausente" en el término es simbolizada en el sitio que le corresponde con un guión (-). De este modo, para una función Boleana de tres variables, AC es representado como "1-0" y BC es representado como "-11".
Cabe agregar que bajo la notación compacta también podemos representar los términos redundantes X, aquellos cuyo valor no importa que sea "1" ó "0" en el diseño de un circuito lógico. Por ejemplo, para la siguiente Tabla de Verdad en la cual se muestran dos términos redundantes marcados con una "X", los cuales corresponden a los minterms AB·CD y ABCD que en notación compacta vendrían siendo m9 y m14:
la representación en notación compacta usando minterms será:
f(A,B,C,D) = Σm(4,8,10,11,12,15) + d(9,14)
El método Quine-McCluskey, el cual hace uso repetido del axioma Boleano A+A=1, involucra la siguiente secuencia de pasos, la cual es obvia para quien haya tenido ya alguna práctica en el uso de los mapas de Karnaugh:
Primer paso: Se van agrupando los minterms dependiendo de la cantidad de "unos" que tengan en su representación binaria. Esta cantidad es conocida como el índice de la representación (0000 tiene un índice de 0, 0010 y 1000 tienen ambas un índice de 1, 1010 y 0011 y 1001 tienen las tres un índice de 3, y 1111 tiene un índice de 4). Así, en la siguiente expresión Boleana de cinco variables:
F(p,q,r,s,t) = Σm(0,1,3, 4,6,11,14,15,16,18,24,27,28,31)
el agrupamiento de los términos de acuerdo con sus índices es el que se muestra a continuación:
Segundo paso: Se van comparando los grupos vecinos (vecinos en lo que respecta a sus índices), y se van reemplazando pares de términos que difieren únicamente en un solo "1", los cuales son conocidos como términos adyacentes. Este proceso de combinación requiere poner el guión que simboliza tanto el "0" como el "1" (lo cual corresponde directamente al "agrupamiento" de dos celdas vecinas en el mapa de Karnaugh) al llevarse a cabo la combinación, como lo muestra el siguiente esquema en el cual los valores ABCD=1110 y ABCD=1111 se pueden combinar como 111- por diferir los índices de ambos en solo un "1":
Podemos reemplazar dos términos adyacentes cualesquiera que contengan un solo guión en una posición que corresponda al bit no apareado. Al ir llevando a cabo este procedimiento, para comodidad nuestra, podemos ir "checando" con una "palomita" o "marcando" con una "equis" de alguna manera los minterms que van siendo utilizados para crear términos comunes para que así no sean incluídos nuevamente por equivocación.
Tercer paso: Repetimos la búsqueda hasta que no sea posible encontrar más términos adyacentes. Dos términos adyacenes que contengan guiones son considerados adyacentes solo sí todas las posiciones con guiones se correspondan en ambos términos y todas excepto una sola posición literal contengan el mismo valor. En la expresión Boleana que estamos utilizando como ejemplo, estos pasos aparecen resumidos en la manera que se muestra a continuación (obsérvese que tenemos aquí dos listas, la primera que aparece en el extremo izquierdo, y la lista puesta en el medio y la cual fue obtenida de la primera):
Cuarto paso: Removemos todos los términos que aparezcan duplicados y listamos los términos que sobrevivieron al proceso, indicando cuáles de los minterms originales están cubiertos por los términos sobrevivientes.
Quinto paso: Seleccionamos el número mínimo de implicantes residuales necesarios para cubrir todos los minterms, lo cual puede ser algo laborioso de encontrar conforme aumenta el número de variables. Los últimos pasos están resumidos en el siguiente arreglo reticular en el cual listamos todos los implicantes primarios (en la columna extrema izquierda) y todos los minterms de la función (en el renglón superior), en donde cada minterm cubierto por algún implicante primario es marcado en la posición apropiada:
Sexto y último paso: Recogemos el conjunto seleccionado de implicantes primarios para generar una expresión Boleana minimizada.
Necesariamente, cualquier minimización obtenida bajo el método de Quine-McCluskey contendrá únicamente implicantes primarios.
Tanto el mapa de Karnaugh como el método de Quine-McCluskey se pueden extender para llevar a cabo la simplificación de circuitos lógicos de varias entradas y varias salidas, o sea de entradas múltiples y salidas múltiples, tales como un diseño de tres entradas A, B y C, y dos salidas H1 y H2, cuya Tabla de Verdad sea la siguiente:
Sin embargo, esta situación no involucra la invención de ningún nuevo tipo de mapa de Karnaugh. En realidad, la situación mostrada en este ejemplo requiere de la construcción de dos mapas de Karnaugh, uno para la salida H1 y el otro para la salida H2. Esto es obvio cuando nos damos cuenta de que la Tabla de Verdad mostrada es un resumen de dos Tablas de Verdad, una para H1 y la otra para H2. Del mismo modo, un circuito lógico con tres entradas y cinco salidas requerirá de la construcción de cinco mapas de Karnaugh, uno para cada una de las cinco salidas. La cantidad de salidas de un circuito lógico es la que determina la cantidad de mapas de Karnaugh que serán requeridos para tratar de minimizar los componentes que serán usados. En el ejemplo mostrado, tenemos dos mapas, el mapa correspondiente a la salida H1:
y el mapa correspondiente a la salida H2:
Una vez que tenemos todos los mapas de Karnaugh a la mano, tenemos dos opciones: la primera consiste en tratar de simplificar lo más posible los circuitos correspondientes a cada una de las salidas de manera independiente consultando única y exclusivamente el mapa de Karnaugh que corresponda a cada salida, y es la opción más fácil de todas. La segunda opción consiste en tratar de simplificar las salidas buscando los términos comunes que aparezcan en los mapas y que se puedan agrupar con el fin de evitar repeticiones innecesarias mediante el uso de sub-circuitos que pueden alimentar en forma común a dos o más salidas, lo cual requiere tener todos los mapas lado a lado. A continuación se muestran los mapas de Karnaugh para un circuito lógico con cuatro variables de entrada a, b, c y d, y dos salidas X y Y, en los cuales viéndolos juntos a primera vista se antojan algunas simplficaciones posibles notando las celdas que tienen en común:
La aplicación de los conceptos aquí aprendidos a un circuito multi-salidas para lograr su simplificación óptima se puede convertir en un asunto algo elaborado. Sin embargo, no se entrará más a fondo en un estudio sobre una extensión de la técnica del mapa de Karnaugh (y mucho menos del método de Quine-McCluskey) bajo hoy anticuadas filosofías de economización porque en la práctica con el bajo costo del "hardware" puede salir más caro tener a un ingeniero consumiendo varios días o inclusive varias semanas de su tiempo para lograr la simplificación de un circuito pese a que con el bajo costo actual de la microelectrónica no se logre un ahorro que justifique la inversión del tiempo de ingeniería en estos ejercicios intelectuales. Puesto de otra manera, en la simplificación de circuitos lógicos elaborados hay que tener en cuenta también el factor costo para saber si vale la pena invertir tiempo valioso de ingenieros competentes cuando hay otras técnicas (como el uso de las memorias ROM y PROM que serán tratadas en un capítulo posterior) que han hecho obsoletas las inversiones excesivas en tiempo de diseño. Si en otros tiempos por el alto costo inclusive de un simple inversor lógico NOT construído con un bulbo electrónico como el popular 6SN7 (utilizado ampliamente en la construcción de radios de bulbos y televisores de blanco y negro) era deseable e inclusive necesario economizar todas las funciones lógicas que fuese posible en un diseño, esto es ya una cosa del pasado, y hoy hay que adaptarse a los nuevos tiempos.