PROBLEMA: La Tabla de Verdad para un circuito lógico es la siguiente:
¿Cuál es el diagrama para el circuito de acuerdo con esta Tabla de Verdad?
En este caso, puesto que hay menos unos que ceros, es más conveniente diseñar alrededor de los unos, o sea usando minterms. Obtenemos primero de la Tabla de Verdad los minterms requeridos:
La salida está dada por:
Salida = f2 + f5
Salida = A·B·C + + A·B·C
Salida = A·B·C + + A·B·C
El diagrama del circuito correspondiente es como se muestra a continuación:
PROBLEMA: Diseñar un "OR-exclusivo" de tres entradas obteniendo primero su expresión de salida a partir de una Tabla de Verdad y dibujando a continuación el circuito requerido. Diseñar alrededor de los "ceros" (usando maxterms). No es necesario simplificar la expresión Boleana obtenida.
Puesto que en un "OR-exclusivo" la salida es "0" únicamente cuando todas las entradas son iguales, la Tabla de Verdad requerida será la siguiente:
Diseñando alrededor de los ceros, obtenemos por medio de maxterms la siguiente expresión de salida:
Salida = f1f8
Salida = (A + B + C) ∙ (A + B + C)
El circuito correspondiente a la expresión obtenida es el siguiente:
PROBLEMA: Obtener la Tabla de Verdad del siguiente circuito; y a partir de la misma obtener la salida en función de los minterms.
Considerando todas las combinaciones posibles de "unos" y "ceros" en las entradas A y B obtenemos la siguiente Tabla de Verdad:
Notamos que esta configuración produce un "1" a la salida siempre que ambas entradas son iguales.
El circuito anterior frecuentemente se representa de la siguiente manera:
Esta función es conocida comúnmente como la función NOR-EXCLUSIVO y al igual que su contraparte el OR-EXCLUSIVO también juega un papel importante dentro de los circuitos lógios. Su salida está dada por la expresión:
Salida = f1 + f4
Salida = A·B + AB
Salida = A·B + AB
PROBLEMA: La siguiente Tabla de Verdad corresponde a una configuración con salidas múltiples. Obtener un diagrama para dicha configuración que produzca la Tabla de Verdad mostrada.
Obtenemos primero una expresión para la salida H1 usando minterms por conveniencia (para H1 hay más maxterms que minterms; sólo hay dos minterms):
H1 = ABC + ABC
Obtenemos ahora H2 usando maxterms por conveniencia (para H2 hay más minterms que maxterms; sólo hay dos maxterms):
H2 = (A + B + C)(A + B + C)
Removiendo los paréntesis y simplificando lo más posible:
H2 = AA + AB + AC + B·A + B·B + B·C + CA + CB + CC
H2 = AB + AC + A·B + B + B·C + AC + BC
H2 = AB + AC + B(A + 1) + B(C' + C) + AC + AC
H2 = AC + AC + B
El diagrama de este circuito será como el que se muestra a continuación:
Obsérvese con detenimiendo la forma en la cual fue construído este circuito lógico de salidas múltiples. Primero se construyó un arreglo simétrico de líneas horizontales del cual se pueden obtener de inmediato en forma selectiva las señales A, A, B, B, C y C. Con este acomodo, no fue ningún problema el obtener de las líneas horizontales los términos ABC y ABC usados para obtener la salida de H1, así como los términos AC , AC y B, usados para obtener la salida de H2, con el simple recurso de tender líneas verticales desde los puntos seleccionados hacia los bloques AND en donde se producirán los productos selectivos de los términos, tras lo cual fue asunto fácil enviar los resultados intermedios hacia los bloques OR para obtener el resultado final. Este acomodo selectivo de líneas horizontales y verticales asemeja el arreglo rectangular de renglones y columnas que un matemático conoce como una matriz, aunque aquí estamos utilizando el término con una connotación meramente gráfica. Este arreglo se puede extender fácilmente hacia circuitos lógicos con una mayor cantidad de entradas y con una mayor cantidad de salidas. Cuando en un circuito lógico tanto las líneas de entrada como las líneas de salida del circuito son numerosas, en vez de perder lamentablemente el tiempo tratando de encontrar el circuito lógico óptimo que requiera la menor cantidad posible de bloques OR, NOT y AND, es mil veces preferible y mucho más económico recurrir a un arreglo similar al mostrado arriba implementado en un circuito integrado de bajo costo conocido como el ROM (el cual será estudiado posteriormente más a fondo en otro capítulo), en el cual los puntos de "conexión" de las líneas horizontales con las líneas verticales son seleccionados según se requiera ya sea por un proceso de "soldadura" interna de los puntos o por un proceso de "quema de fusibles" internos hasta llegar a lo que se desea. Ello sin tener que recurrir a lo que de otra manera sería un problema pesado en la simplificación de un circuito lógico de salidas múltiples con la finalidad de utilizar la menor cantidad posible de componentes.
PROBLEMA: El sistema de conteo binario es un excelente método para generar diagramas de tiempos que contienen todas las combinaciones posibles de "ceros" y "unos" necesarias para probar circuitos lógicos con varias entradas. Construír un diagrama de tiempos para probar un circuito lógico con entradas A, B, C y D.
A continuación tenemos el siguiente conteo binario para las cuatro variables:
Los contenidos de esta tabla se pueden vaciar directamente en un diagrama de tiempos múltiples para obtener los diagramas de tiempo de cada una de las entradas "alineados" de forma tal que se vayan produciendo al ir de un tiempo a otro todas las combinaciones posibles de "unos" y "ceros":
PROBLEMA: El diagrama de tiempos en lógica positiva de un circuito se muestra a continuación. ¿Cuál es la configuración del circuito? (Todas las combinaciones posibles están contenidas en el diagrama de tiempos).
Para la resolución de este problema, construímos primero la Tabla de Verdad directamente a partir del diagrama de tiempos proporcionado:
En este caso, puesto que hay menos "unos" que "ceros", es más fácil obtener el circuito deseado por medio de minterms (diseñando alrededor de los unos):
Salida = f1 + f3 + f4
Salida = A·B·C + A·B·C + + A·B·C
El diagrama del circuito es el siguiente, construído directamente a partir de la expresión obtenida:
PROBLEMA: En los siguientes dibujos representativos de relevadores electromecánicos como los que fueron introducidos al principio del segundo capítulo de este libro (Las Tres Funciones Lógicas Básicas):
tenemos en el extremo superior izquierdo un relevador inactivo (obsérvese que la entrada es un "0", indicando con ello la aplicación de cero voltaje a la bobina del relevador) con lo cual el voltaje +V pasa a las dos salidas complementarias del relevador como "1" y como "0" de la manera mostrada, mientras que en el extremo superior derecho tenemos al mismo relevador energizado (obsérvese que la entrada a la bobina del relevador es un "1") con lo cual su contacto normalmente cerrado se abre y su contacto normalmente abierto se cierra, invirtiéndose los valores "1" y "0" en sus salidas complementarias. Tomando esto en cuenta, analizar el comportamiento del circuito formado por los tres relevadores electromecánicos cuyas entradas son A, B, C, D y E, y cuya salida es OUT.
Nuestro análisis comienza con el relevador electromecánico cuyas entradas son A y B, y cuya salida denominaremos YAB. Si A=0 el relevador estará inactivo, y si A=1 el relevador será energizado dejando pasar el valor que tenga B a la salida YAB. Obsérvese que la salida YAB sólo puede ser "1" si tanto A como B son "1", de lo contrario será "0". Esto es una función AND, y la salida será YAB=AB, la cual alimenta a la bobina del segundo relevador electromecánico, el cual exhibe un comportamiento idéntico al del primer relevador, ya que tanto la entrada YAB a su bobina como el valor de C tienen que ser ambos "1" para que la salida del relevador que denominaremos YC sea "1", lo cual es también una función AND. Con esto tenemos que:
YC = YABC = ABC
Nos queda un problema al considerar la salida del tercer relevador electromecánico con entradas D y E, la cual está conectada al mismo punto eléctrico de la salida del circuito OUT al cual está conectada también la salida YC del segundo relevador. No nos lleva mucho tiempo darnos cuenta que si C=1 y E=0 o bien si C=0 y E=1, en caso de energizarse ambas bobinas del segundo y del tercer relevador se creará un corto circuito en OUT, aterrizando directamente un voltaje de "1" a tierra. Hay dos formas de evitar este cortocircuito. La primera es haciendo que las entradas C y E sean iguales todo el tiempo, lo cual requiere que C=E. Y como la salida del tercer relevador es YDE=DE, entonces la salida lógica del circuito será:
OUT = DE = DC
La otra forma de evitar un cortocircuito es añadiendo diodos rectificadores en las terminales C y E (que podríamos suponer vienen ya añadidos desde antes y por ello no aparecen en el diagrama del circuito) con lo cual aunque C y E tengan valores lógicos diferentes no habrá ya un cortocircuito. En este caso, los diodos rectificadores convertirán la juntura en una conexión OR cuya salida será:
OUT = YC + DE
OUT = ABC + DE
OUT = ABC + DE
PROBLEMA: En el texto principal del capítulo anterior se había hablado acerca de la "lógica alambrada" (wired logic), la cual permite que las salidas de aquellas funciones lógicas que hayan sido fabricadas bajo la tecnología del transistor con "colector abierto" se puedan conectar directamente al mismo punto, actuando el punto de juntura como una función AND para las salidas producidas por los bloques lógicos, destacándose estos componentes con el símbolo de un diamante con una barra horizontal debajo del mismo dibujado dentro de tales bloques lógicos, cerca de las salidas de los mismos, como lo mostró el ejemplo de los dos NOTs conectados de la siguiente manera:
En dicho ejemplo, la salida de cada NOT es A y B, respectivamente, y como la lógica alambrada se encarga de efectuar una operación AND sobre dichas salidas, la salida común del circuito será igual a Y=( A)(B) o bien Y=A+B utilizando las leyes de DeMorgan, con lo cual queda evidenciado que este circuito se comportará como un NOR. Obtener la expresión Boleana para las salidas de los siguientes circuitos, notándose que se están utilizando componentes con "lógica de colector abierto". Se sobreentiende que del punto de juntura común en la salida Y hay una resistencia conectada hacia el polo positivo de la fuente de voltaje:
1)
2)
3)
En el primer caso, la salida de cada NOR es A+B y C+D, lo cual es "multiplicado" operación AND por la lógica alambrada, con lo cual la salida del circuito será:
Y = A+B ∙ C+D
En el segundo caso, la salida de cada NAND es A·B y C·D, lo cual es " multiplicado" en operación AND por la lógica alambrada, con lo cual la salida del circuito será:
Y = A · B ∙ C · D
En el tercer caso, la salida del circuito será:
Y = (A + B) ∙ C · D
PROBLEMA: El Medio Sumador.- Dadas las palabras A=0011 y B=0101 (las cuales contienen todas las combinaciones posibles de "unos" y "ceros" para dos terminales de entrada A y B de un circuito lógico), y llevando a cabo una suma aparejada de cada bit sin afectar los bits restantes, o sea una suma individual bit-por-bit, encontrar el bloque básico requerido para poder sumar en el sistema binario (¡esta no es una suma Boleana, es una auténtica suma aritmética!). Encontrar también las ecuaciones Boleanas correspondientes a este tipo de circuito.
Sumando las palabras dadas bit por bit sin afectar los bits restantes, ni los que están a la izquierda ni los que están a la derecha, tendríamos la siguiente situación en nuestras manos:
Esto lo podemos leer de la siguiente manera comenzando con los bits del extremo derecho, A=1 y B=1. Procediendo en forma idéntica a la manera en la cual llevaríamos a cabo la suma en nuestro sistema decimal, con la única variante de que el sistema de conteo es binario en lugar de decimal, diríamos lo siguiente: "1 más 1 es igual a 10 -recuérdese que esta sí es una suma binaria; entonces anotamos 0 y llevamos 1". Resulta obvio que vamos a requerir de dos terminales de salida, una terminal que denominaremos "Anotar" (en inglés a esta terminal se le llama Sum o simplemente S) y una terminal de "Llevar" (en inglés a esta terminal se le llama Carry o simplemente C), con los valores Anotar=0 y Llevar=1 para A=1 y B=1. Para la combinación de bits A=1 y B=0 decimos "1 más 0 es igual a 1; entonces anotamos 1 y llevamos 0", con lo cual las salidas deben ser Anotar=1 y Llevar=0. La combinación de bits A=0 y B=1 tiene un efecto similar. Por último, la combinación de bits A=0 y B=0 simplemente produce los valores Anotar=0 y Llevar=0. Con esto, tenemos todas las combinaciones posibles para poder construír una Tabla de Verdad para un circuito con dos entradas A y B y dos salidas Anotar y Llevar.
Para realizar las operaciones "Anotar" y "Llevar", se requiere un OR-exclusivo para la operación de "Anotar" y se requiere de un AND para la operación de "Llevar", según se puede observar arriba. El diagrama para el circuito requerido es el siguiente:
Las ecuaciones Boleanas para el Medio-Sumador, conocido en inglés como el Half-Adder, serán:
Anotar = AB + AB
Llevar = AB
Llevar = AB
El bloque anterior frecuentemente se simplifica de alguna manera como la siguiente, encerrándolo en una "caja negra":
Como se indica arriba, dicho bloque se conoce como el Medio-Sumador y desempeña un papel importante como tal en su función.
Usando dos Medio-Sumador y un OR, se puede construír un Sumador-Completo que lleve a cabo la suma binaria (no la suma boleana) de dos bits A y B, siendo éste el bloque fundamental de todos los sumadores electrónicos usados en la actualidad, y siendo la base fundamental de la Unidad de Aritmética y Lógica ALU (Arithmetic Logic Unit) de cualquier computadora.
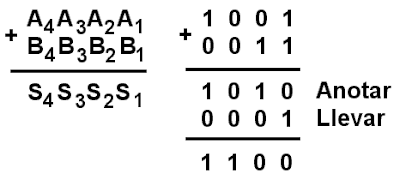
PROBLEMA: Diseñar un circuito para calcular la suma binaria de dos números A y B de 4 bits cada uno. Utilizar las palabras A4A3A2A1=1001 y B4B3B2B1=0011 para demostrar su funcionamiento.
Este problema representa una de las metas importantes en las que hemos venido trabajando desde el inicio de esta obra: la realización de un circuito, construído a base de funciones lógicas básicas, que sea capaz de llevar a cabo la operación aritmética más esencial de todas, la suma, en el sobreentendido de que esta operación se tendrá que llevar a cabo en el lenguaje binario de "unos" y "ceros" que es el lenguaje que entienden las máquinas. El asunto de la conversión automática de nuestros números decimales a números binarios es algo que tendrá que ser postpuesto en espera de dar cobertura a otro tipo de circuitos que sean capaces de secuenciar operaciones de "unos" y "ceros", aquí nos conformaremos con el diseño de un circuito que sea capaz de ponder inmediatamente a su salida el resultado de la suma binaria de dos números puestos a su entrada. Si somos capaces de diseñar un circuito así, el problema de poder llevar a cabo la operación de multiplicación con funciones lógicas básicas quedará resuelto en su esencia, puesto que una multiplicación en realidad no es más que la suma repetitiva de un multiplicando por la cantidad de veces especificada por el multiplicador.
En este problema, en contra de lo que se ha estado llevando a cabo en todos los problemas anteriores, el flujo de las señales se llevará a cabo de derecha a izquierda; esto en virtud de que en la suma aritmética de dos números como 582973 y 416912, empezamos sumando los dígitos que están más a la derecha, en este caso el 3 y el 2, continuando con los dígitos que siguen a la izquierda, en este caso el 7 y 1, y así sucesivamente. En el caso de la suma aritmética binaria, el procedimiento es el mismo. De cualquier modo, desde el punto de vista de la electrónica digital del circuito, es irrelevante la forma de dibujar el diagrama esquemático del circuito, porque aún si lo construyéramos con un flujo de señales yendo de derecha a izquierda tal y como ocurre en el diagrama, todo lo que tendríamos que hacer con el circuito físico sería voltear la tablilla horizontalmente con lo cual el flujo de señales será de derecha a izquierda aunque la suma se seguirá llevando a cabo exactamente de la misma manera.
El sumador será construído utilizando como "caja negra" el Medio-Sumador visto en un problema previo, el cual será simbolizado simplemente como MS (+) en el diagrama. Llamando a S4S3S2S1 el resultado de la suma binaria, el circuito deseado tendrá la siguiente configuración:
A continuación tenemos lado a lado la suma binaria simbólica y la suma binaria llevada a cabo con los números 1001 y 0011:
Podemos imaginar a este circuito subdividido en cuatro "columnas" imaginarias, cada una de las cuales representa una "unidad" que se repite en forma idéntica. Con la excepción de la primera columna, todas las demás columnas representan una configuración semejante en su estructura, que es la siguiente:
En el diagrama del circuito completo se han representado con color rojo los "unos" y los "ceros" que se van produciendo a través de toda la configuración hasta llegar a la salida. El lector puede percatarse por sí mismo de que cualquier otra combinación de dos números binarios de cuatro bits será procesada aritméticamente en forma correcta por este circuito produciendo la suma binaria de ambos. Podemos representar cada una de las columnas imaginarias mostradas en este circuito como una "caja negra" como la siguiente, en donde hemos utilizado la letra griega Σ (sigma) dentro de la caja por ser la letra frecuentemente utilizada por los matemáticos para indicar una sumación:
La terminal "Llevar salida" (Carry Output) es la que se utiliza cuando sumamos los bits "1" y "1", los cuales producen dos dígitos binarios en lugar de uno solo: "10". En este caso, el "1" es el que utiliza la función de "Llevar-salida" para que este bit sea sumado en la siguiente columna a los bits más significativos que siguen. La terminal "Llevar entrada" (Carry Input es la que toma en cuenta este bit de "llevar" producido en una columna anterior. Conectar dos "cajas negras" como esta requiere conectar la terminal de "Llevar salida" de un bloque a la terminal "Llevar entrada" del bloque que le sigue a la izquierda. Este bloque es mejor conocido como el Sumador Completo, y es el bloque que tenemos que ir conectando en serie (en "cascada") con otros bloques iguales para ir aumentando la capacidad de la magnitud del número que podrá ser manejado por el sumador binario. De aquí en delante, aumentar la capacidad del sumador completo para poder sumar números de 16 bits, de 32 bits, de 62 bits, de 124 bits o más, no involucrará ningún diseño nuevo, solo requerirá ir conectando una cantidad mayor de "cajas negras" a la cantidad deseada.
Nótese que si le presentamos al circuito los números A=1111 y B=1111, el primer bit de la suma resultante S=11110 se pierde por falta de capacidad de almacenamiento en los registros. Esta condición se conoce como sobreflujo (overflow). El bit que aparece como "1" en la función "Llevar" de la columna en el extremo izquierdo del circuito se puede usar para indicar que dicha condición de sobreflujo ha ocurrido en una operación.
En un diagrama de un sumador binario de 4 bits en el cual el flujo de las señales vaya no de derecha a izquierda (siguiendo la secuencia humana en la cual se efectúan las operaciones aritméticas de suma) como se configuró arriba sino de derecha a izquierda como se acostumbra hacerlo en la mayoría de los diagramas de los circuitos lógicos, el circuito usando cuatro bloques Sumador-Completo tendría el siguiente aspecto:
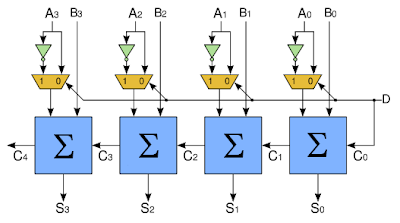
En este circuito, los números binarios a ser sumados son a3a2a1a0 y b3b2b1b0. El resultado de la suma está disponible en la palabra binaria y3y2y1y0. , siendo y3 el bit más significativo (MSB) y siendo y0 el bit menos significativo (LSB). Si hay un sobreflujo como resultado de la suma, este sobreflujo está disponible en la terminal c3 que corresponde a la operación aritmética de "Llevar", lo cual podemos usar ya sea para conectar todo el sumador binario de 4 bits a otro sumador binario de 4 bits igual o para indicar que el resultado de la suma excedió la capacidad de la máquina. Si conectamos dos o más de estos sumadores de 4 bits, todo lo que tenemos que hacer es conectar cada terminal de "Llevar" c3 a la terminal de "Anotar" co del sumador binario de 4 bits que le sigue. La terminal de "Anotar" correspondiente al bit menos significativo es puesta a "0" al no haber un resultado parcial de una suma precedente que considerar. Si lo deseamos, como un ejercicio intelectual podemos construír este sumador binario de 4 bits partiendo de funciones lógicas básicas. Pero tenemos otra opción más atractiva para un diseñista que tenga cosas más importantes que hacer con su tiempo. Podemos comprarlo a muy bajo costo en el mercado, ya construído y entregado en un circuito integrado pequeño que cabe fácilmente en el dedo meñique de la mano. A continuación tenemos el diagrama de un circuito integrado de la familia TTL (véase el Suplemento # 1), el 7483, el cual es un Sumador-Completo de 4-bits (4-Bit Full Adder) como el que acabamos de "construír", con el cual podemos sumar dos números binarios A1A2A3A4 y B1B2B3B4 de cuatro bits, obteniendo la suma binaria respectiva en las terminales S1S2S3S4 con la terminal de "Llevar, salida" (Carry Output, C4, esta es la misma terminal descrita arriba como "Llevar, salida") lista para ser utilizada en caso de que el resultado de alguna suma binaria exceda la capacidad de los cuatro dígitos binarios, y la terminal de "Llevar, entrada" (Carry Input, C0, esta es la misma terminal descrita arriba como "Llevar, entrada") para ser utilizada en caso de que se quieran conectar varios sumadores de 4 bits en cadena, con cada terminal de salida C4 conectada a la terminal de entrada C0 del circuito integrado 7483 que le sigue:
Puesto que aquí prácticamente todas las terminales del circuito integrado están siendo utilizadas a su máxima capacidad dejando únicamente dos terminales disponibles, la terminal 5 y la terminal 12, es precisamente en estas dos terminales en donde se le aplican al circuito integrado los polos positivo (+) y negativo (-) de la fuente de poder.
PROBLEMA: Construír una Tabla de Verdad para un Sumador-Completo, y a partir de la misma obtener las expresiones Boleanas para las funciones "Anotar" y "Llevar" en función de minterms. (La función "Llevar" se refiere en este caso a la función "Llevar salida".)
Por las características del Sumador-Completo, la Tabla de Verdad debe ser forzosamente como la que se muestra:
En base a esta Tabla de Verdad, las expresiones Boleanas deseadas serán:
Anotar = A·B·C + ABC + A·B·C + ABC
Llevar = ABC + ABC + ABC + ABC
Llevar = ABC + ABC + ABC + ABC
PROBLEMA: Demostrar que para un Sumador-Completo:
Llevar = AB + (A+B) ·A·B·C
Anotar = [(A + B)·A·B + C][(A + B)ABC]'
en donde C es la terminal de "Llevar, salida". (Sugerencia: Considerar la salida de un OR-EXCLUSIVO como (A+B)·A·B.)
Trazando el flujo de las señales a través del Sumador-Completo considerando la acción que llevan a cabo los Medio-Sumador:
obtenemos primero de inmediato la expresión Boleana para terminal Llevar que pasará un bit de "1" en caso de que la suma binaria produzca "10" por ser ambas entradas A y B iguales a "1":
Llevar = AB + (A+B) ·A·B·C
Y en lo que respecta a la función Anotar que viene de la acción del OR-EXCLUSIVO contenido en el Medio-Sumador inferior:
introduciendo los valores para X1 y X2 obtenemos finalmente:
PROBLEMA: Suma binaria múltiple. ¿Cuál sería la mejor alternativa para poder sumar cuatro números binarios con una extensión de 16 bits?
Aunque es posible diseñar un sumador de dos números binarios con una capacidad para poder manejar números de 16 bits, y hecho esto agregar tres bloques iguales con entradas diferentes para poder sumar cuatro números binarios A, B, C y D, esto sería un desperdicio lamentable de recursos aún es esta época de electrónica microminiaturizada de bajo costo. Existe otra alternativa mucho más eficiente y mucho más económica en términos de recursos de hardware, la cual consiste en ir efectuando totalizaciones parciales hasta llegar al resultado final. Esto requiere de una secuencia de pasos:
(1) Sumar el número A al número B.
(2) Depositar el resultado de la suma de A y B en un registro temporal, al cual llamaremos acumulador, precisamente porque irá acumulando resultados intermedios.
(3) Sumar el número C al número contenido en el acumulador (A+B), depositando el resultado en el acumulador.
(4) Sumar el número D al número contenido en el acumulador (A+B+C).
Esta alternativa requiere del uso de un solo sumador completo, el cual será utilizado una y otra vez para llevar a cabo la suma múltiple. Al completar estos pasos, el resultado estará contenido en ese registro que estamos llamando acumulador, el cual obviamente debe tener la capacidad para poder "memorizar" un número binario. Esto constituye una motivación para diseñar elementos de memoria. Pero además necesitamos de algún secuenciador que sea capaz de efectuar las operaciones señaladas, y que además pueda ser modificado con facilidad para sumar una cantidad diferente de números, digamos veinte números, para que el diseño del "hardware" no esté atado a una cantidad fija de números. Esto solo lo podemos lograr usando algo que sea programable, algo en lo cual podamos escribir las instrucciones necesarias para llevar a cabo una suma binaria múltiple. Estos son, desde luego, los inicios de una máquina programable que sea capaz de ejecutar operaciones aritméticas siguiendo las instrucciones que le sean señaladas. Esta es la motivación para la creación de una computadora.
PROBLEMA: El Medio Substractor.- Dadas las palabras A=10101 y B=01100 (las cuales contienen todas las combinaciones posibles de "unos" y "ceros" para dos terminales de entrada A y B de un circuito lógico), y llevando a cabo una una resta aparejada de los bits encontrar el bloque básico requerido para poder restar bits en el sistema binario, o sea para poder encontrar la diferencia entre dos cantidades en el sistema binario (¡esta es una auténtica resta aritmética!). Encontrar también las ecuaciones Boleanas correspondientes a este tipo de circuito.
A diferencia del problema en el cual se introdujo el caso del Medio-Sumador, aquí se restará la cantidad menor de la cantidad mayor; o sea que se llevará a cabo la operación:
A - B
Restando los números binarios dados, tendríamos la siguiente situación en nuestras manos, acordando en llamar a A el minuendo y a B el substraendo:
Esto lo podemos leer de la siguiente manera comenzando con los bits del extremo derecho, A=1 y B=0. Procediendo en forma idéntica a la manera en la cual llevaríamos a cabo una resta en nuestro sistema decimal, con la única variante de que el sistema de conteo es binario en lugar de decimal, diríamos lo siguiente: "1 menos 0 es igual a 1; entonces anotamos 0 sin necesidad de tener que tomar 'prestado' nada del siguiente bit a la izquierda en el minuendo A". Resulta obvio que vamos a requerir de dos terminales de salida, una terminal que denominaremos "Anotar" (en inglés a esta terminal se le llama Difference o simplemente D) y una terminal de "Pedir prestado" (en inglés a esta terminal se le llama Borrow o simplemente B), con los valores Anotar=1 y Pedir prestado=0 para A=1 y B=0. Para la combinación de bits A=0 y B=0 decimos "0 menos 0 es igual a 0; entonces anotamos 0 y tomamos 'prestado' 0", con lo cual la salidas deben ser Anotar=0 y Pedir prestado=0. En la siguiente combinación A=1 y B=1, decimos "1 menos 1 es igual a 0, entonces anotamos 0 y tomamos prestado 0", con lo cual las salidas deben ser Anotar=0 y Pedir prestado=0. La combinación siguiente, A=0 y B=1, presenta un reto: tenemos que restar 1 de o, lo cual en la aritmética ordinaria sería algo así como tratar de restar 8 de 5. Aunque podríamos recurrir al expediente de inventar aquí los números negativos, recordemos que tal cosa no es necesaria en la escuela primaria; los niños de la primaria aprenden a restar mucho antes de que aprendan en la escuela secundaria el concepto de los números negativos. Hagamos lo mismo que se hace en la escuela primaria; tomamos "prestado" del minuendo en la siguiente cifra posicional a la izquiera una cifra unitaria, disminuyéndolo en la misma cantidad, con el objeto de poder llevar a cabo la resta. Con esto diríamos: "0 menos 1 es igual a 10 menos 1 tomando prestado un 1 de la siguiente columna en el minuendo, con lo cual anotamos un 1 habiendo tomado prestado un 0". En otras palabras, para la combinación A=0 y B=1 requerimos Anotar=1 y Pedir prestado=1.
Para realizar la operación "Anotar" se requiere de un "OR-exclusivo". Usando minterms, la función "Pedir prestado" se logra con la expresión AB. El diagrama para el circuito requerido es el siguiente:
Las ecuaciones Boleanas serán:
Anotar = AB + AB
Pedir prestado = AB
Pedir prestado = AB
El bloque anterior frecuentemente se simplifica de alguna manera como la siguiente, encerrándolo en una "caja negra":
Como se indica arriba, este bloque se conoce como el Medio-Substractor y al igual que el Medio-Sumador también desempeña un papel importante en su función.
Usando dos Medio-Substractor y un OR, se puede construír un Substractor-Completo, el cual junto con el Sumador-Completo forman forman la Unidad Aritmética de casi todas las computadoras digitales usadas hoy en día.
PROBLEMA: Diseñar un circuito para encontrar la diferencia binaria de dos números A y B de 4 bits cada uno. Utilizar las palabras A4A3A2A1=1011 y B4B3B2B1=0101 para demostrar su funcionamiento.
El substractor será construído utilizando como "caja negra" el Medio-Substractor visto en un problema previo, el cual será simbolizado simplemente como MS (-) en el diagrama. Llamando a D4D3D2D1 el resultado de la resta binaria, el circuito deseado tendrá la siguiente configuración:
A continuación tenemos lado a lado la suma binaria simbólica y la suma binaria llevada a cabo con los números 1001 y 0011:
Podemos imaginar a este circuito subdividido en cuatro "columnas" imaginarias, cada una de las cuales representa una "unidad" que se repite en forma idéntica. Con la excepción de la primera columna, todas las demás columnas representan una configuración semejante en su estructura, que es la siguiente:
En el diagrama del circuito completo se han representado con color rojo los "unos" y los "ceros" que se van produciendo a través de toda la configuración hasta llegar a la salida. El lector puede percatarse por sí mismo de que cualquier otra combinación de dos números binarios de cuatro bits será procesada aritméticamente en forma correcta por este circuito produciendo la diferencia binaria de ambos. Podemos representar cada una de las columnas imaginarias mostradas en este circuito como una "caja negra" como la siguiente:
La terminal "Pedir prestado, tomar" (Borrow) es la que se utiliza cuando al tratar de restar un "1" de un "0" en la misma columna es necesario "pedir prestado" de la siguiente columna a la izquierda, al igual que como se acostumbra hacerlo en la resta en el sistema decimal cuando vamos a restar un dígito como 7 de 5 y tenemos que "pedir prestado" una decena (o centena, o lo que se requiera según sea el caso) de la columna de la izquierda para convertir al número 5 en 15 y así poder restar 7 de 15 obteniendo 8. La terminal "Pedir prestado, dar" es la que debe tomar en cuenta este bit de "llevar" producido en una columna anterior con la cual se le ha reducido esta cantidad al darla a la columna a su derecha. Conectar dos "cajas negras" como esta requiere conectar la terminal de "Pedir prestado, tomar" de un bloque a la terminal "Pedir prestado, dar" del bloque que le sigue a la izquierda. Este bloque es mejor conocido como el Substractor Completo, y es el bloque que tenemos que ir conectando en serie (en "cascada") con otros bloques iguales para ir aumentando la capacidad de la magnitud del número que podrá ser manejado por el substractor binario. De aquí en delante, aumentar la capacidad del substractor completo para poder restar números de 16 bits, de 32 bits, de 62 bits, de 124 bits o más, no involucrará ningún diseño nuevo, solo requerirá ir conectando una cantidad mayor de "cajas negras" a la cantidad deseada, al igual que como ocurrió con el Sumador-Completo.
PROBLEMA: Construír una Tabla de Verdad para un Substractor-Completo, y a partir de la misma obtener las expresiones Boleanas "Anotar" y "Pedir prestado" en función de minterms.
Intuyendo las características del Substractor-Completo, la Tabla de Verdad será como sigue:
En base a esta Tabla de Verdad, las expresiones Boleanas deseadas serán:
Anotar = A·B·C + ABC + A·B·C+ ABC
Pedir prestado = A·B·C + ABC + ABC + ABC
Pedir prestado = A·B·C + ABC + ABC + ABC
PROBLEMA: Demostrar que para un Substractor-Completo:
Anotar = (AC + AC)B + (AC + A·C)B
Pedir prestado = (AC + A·C)B + AC
Pedir prestado = (AC + A·C)B + AC
en donde C es la terminal de "Pedir prestado, dar". (Considérese la salida del OR-EXCLUSIVO como AB+AB.)
Trazando el flujo de las señales a través del Substractor-Completo considerando la acción que llevan a cabo los Medio-Substractor:
del flujo de señales se obtiene primero que, para la función Anotar:
Anotar = X1X2 + X1X2
Anotar = (AC + AC)B + [AC + AC]'B
Usando en el segundo término las leyes de DeMorgan, se tiene que:
Anotar = (AC + AC)B + (AC)'(AC)'B
Aplicando las leyes de DeMorgan:
Anotar = (AC + AC)B + (A + [(C)]')([(A)]' + C)B
Anotar = (AC + AC)B + (A + C)(A + C)B
Anotar = (AC + AC)B + (AA + A·C + AC + CC)B
Anotar = (AC + AC)B + (AC + A·C)B
Del mismo modo, para la función "Pedir prestado, dar":
Pedir prestado = X3 + AC
Pedir prestado = X1X2 + AC
Pedir prestado = [AC + AC]'B + AC
Usando la misma simplificación del segundo término llevada a cabo en la función Anotar tenemos finalmente para Pedir prestado:
Pedir prestado = (AC + A·C)B + AC
PROBLEMA: Diseñar un circuito con capacidad de 3 bits que pueda funcionar tanto como "sumador completo" como "substractor completo", tomando como base la técnica del "2-complemento".
Usando la técnica del 2-complemento, la combinación en un solo circuito lógico de las capacidades de un sumador y de un substractor de números binarios se puede llevar a cabo con facilidad de la manera mostrada en el siguiente circuito que es esencialmente un sumador completo de 4 bits con una de sus entradas modificadas para poder convertir al número A en un número negativo en su representación como 2-complemento y poder así llevar a cabo la operación aritmética de resta B-A:
La conversión del Sumador Completo a un circuito que pueda actuar también como Substractor significa que la capacidad numérica quedará reducida a 3 bits, habido el hecho de que el bit más significativo (MSB) tendrá que ser adjudicado para el manejo del signo aritmético que podrá ser positivo (+) o negativo (-1). En el diseño del circuito, el Sumador Completo estudiado en los problemas anteriores es representado aquí como una "caja negra" de color azul. Sin las modificaciones mostradas arriba, al ponerle los números binarios A3A2A1A0 y B3B2B1B0 a su entrada (los cuales suponemos positivos ambos) la suma binaria aparecerá en la salida S3S2S1S0 del circuito.
En el circuito modificado, si A=A3A2A1A0 es un número positivo, entonces se pondrá un "0" en la línea D para que en cada pequeño multiplexer (dibujados con color café) con la condición de "0" puesta en D todos los bits del número A pasen intactos a los bloques Sumador Completo. Tenemos así un sumador binario de 4 bits que lleva a cabo la operación A+B. Y si queremos llevar a cabo la resta B-A, entonces se pondrá un "1" en la línea D para que en cada bloque multiplexer con la condición de "1" puesta en D los bits del número A pasen invertidos lógicamente (por la acción de los NOTs de color verde) al conjunto sumador de bloques, y como el "1" que se está poniendo en la línea D también entra al mismo tiempo en el primer Sumador Completo como una señal de Llevar (Carry), esto equivale a sumar un "1" al resultado de todo, que podemos considerar sumado al 1-complemento de A, con lo cual se tiene el 2-complemento de A sumado a B, o sea B-A por ser A un número binario negativo en 2-complemento.
El circuito, tal y como está dado, no está preparado para sumar dos números negativos. Sin embargo, puesto que la suma de dos números negativos es igual a la simple suma de las magnitudes de los números conservando el signo negativo (-) en la respuesta final, las modificaciones requeridas para que nuestro circuito mejorado pueda hacer operaciones aritméticas con dos números binarios cualesquiera que sean sus signos son modificaciones mínimas.
En una computadora digital existe otra manera de que se puedan llevar a cabo las operaciones aritméticas de dos números cualesquiera que sean sus signos usando un simple Sumador Completo sin modificación alguna, y esto es por la vía de la programación. Las instrucciones del programa escrito por el programador serían las encargadas de llevar a cabo las operaciones necesarias de 2-complementación, pasándole los números binarios ya "transformados" al Sumador Completo. Esto no es más que uno de muchos ejemplos de algo que se encuentra en el fondo de cualquier decisión de diseño para la arquitectura de cualquier computadora: escoger entre la opción de implementar alguna función por la vía de la programación sin agregarle nuevos circuitos o componentes a la máquina, o implementar la misma función por la vía de la adición de más componentes y circuitos. La enorme ventaja de la segunda opción es que el procesamiento de información por la vía de circuitos electrónicos especializados es mucho más rápida que implementarla por la vía de la programación, lo cual requerirá la utilización de varios ciclos de instrucción en el programa de la máquina para obtener el mismo resultado. Es por esta razón, aunada al dramático abaratamiento de los circuitos en los cuales se implementa la microelectrónica de la lógica digital, que la tendencia ha sido transferir la mayor cantidad posible de funciones a la máquina, quitándole cada vez más y más un peso de encima al programador.