4: Problemas resueltos

PROBLEMA: Verificar los dos teoremas de DeMorgan mediante el uso de diagramas de subconjuntos.

Empezaremos por la verificación del teorema de DeMorgan que dice:

A + B = A · B

Un diagrama de subconjuntos nos permite localizar A + B de la siguiente manera:

Por otra parte, de los diagramas de subconjuntos de A y B:

vemos de la intersección de los mismos (que viene siendo el producto Boleano de A y B) que A·B es igual a:

Esto comprueba el teorema de DeMorgan que se deseaba verificar.

Ahora continuamos con el teorema de DeMorgan que dice:

A · B = A + B

Un diagrama de subconjuntos nos permite localizar A · B de la siguiente manera:

Por otra parte, de los diagramas de subconjuntos de A y B que tenemos arriba, vemos que la suma de los mismos A+B es igual al diagrama superior derecho. Esto comprueba el otro teorema de DeMorgan que se deseaba verificar.

PROBLEMA: Mostrar todos los términos posibles del doble producto ABC usando un diagrama de subconjuntos, escribiendo dentro de cada celda el término que le corresponda (como ABC, ABC, etc.)

Para la resolución de este problema, resulta conveniente tener a la mano los diagramas de subconjuntos para cada una de las variables considerando que el sistema estará formado por tres variables en total:

Con estos tres diagramas a la mano, resulta fácil elaborar el diagrama de subconjuntos mostrando todos los términos posibles del doble producto ABC:

PROBLEMA: Usando diagramas de subconjuntos, diseñar una máquina que produzca las siguientes salidas.

Esta máquina se puede lograr juntando los productos básicos ABC, ABC, ABC y ABC, pero en este problema se trata de construír una máquina más sencilla.

Un vistazo al diagrama de subconjuntos producido por la Tabla de Verdad proporcionada demuestra que dicho diagrama se puede descomponer en la suma de otros sub-diagramas que representan expresiones más sencillas:

En base a esto, la salida correspondiente a la misma máquina pero construída de una manera más sencilla será:

Salida = AB + AC + BC

Obsérvese que con mera álgebra Boleana no es posible "ver" fácilmente esta simplificación.

Esta máquina puede ser vista como una máquina analizadora de votos, puesto que la salida será "1" cuando una mayoría de las entradas A, B, C sean "1". Y desde luego, el principio de la misma puede ser extendido a más de tres entradas.

PROBLEMA: Usando diagramas de subconjuntos, diseñar la máquina más sencilla posible cuya Tabla de Verdad sea la siguiente:

Tomando en cuenta las entradas que producen un "1" a la salida, de la Tabla de Verdad obtenemos el siguiente diagrama de subconjuntos (usando el mismo orden de acomodos que en los problemas previos) que destaca los seis términos A·B·C, ABC, ABC, AB·C, ABC y ABC:

Podemos agrupar los términos ABC', ABC y A·B·C obteniendo la región común a las variables B y C, o sea B+C, y tomando tras esto la intersección de esta región con la región que corresponde a la variable A:

Podemos agrupar también los términos ABC y AB·C:

Esto deja a un solo término solitario, el término ABC:

Sumando las tres regiones obtenemos la expresión final para la máquina simplificada:

Salida = A(B + C) + AB + ABC

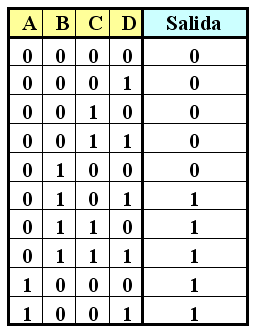
PROBLEMA: Dado un circuito cuya Tabla de Verdad es la siguiente:

construír el mapa de Karnaugh que le corresponde, mostrando en el mapa todas las entradas correspondientes tanto de los "unos" como de los "ceros".

El contenido de cualquier Tabla de Verdad se puede vaciar directamente a un mapa de Karnaugh, y viceversa. La Tabla de Verdad y el mapa de Karnaugh son en realidad dos formas diferentes de representar exactamente la misma información. Podemos empezar con la construcción del mapa poniendo un "1" en todos los casilleros del mapa que correspondan a los minterms, por ejemplo ABCD, A·B·CD, etc., y una vez que hayamos vaciado todos los minterms en el mapa podemos simplemente llenar el resto de los casilleros con "0". Para la Tabla de Verdad proporcionada, vaciando los "unos" en los lugares que les corresponden y vaciando los "ceros" en los lugares que les corresponden, el mapa de Karnaugh será:

PROBLEMA: Representar, usando mapas de Karnaugh para cuatro variables, las siguientes expresiones que contienen minterms:

1) ABCD + ABCD + ABCD + A·B·CD + A·B·CD

2) ABCD + AB·C·D + ABC·D + A·B·CD + A·B·C·D

Los mapas de Karnaughg para las expresiones dadas serán como se muestra a continuación:

1)

2)

PROBLEMA: La Tabla de Verdad para un circuito lógico es como se muestra a continuación:

Usando minterms, dibujar su mapa de Karnaugh correspondiente.

De acuerdo con la Tabla de Verdad proporcionada, trabajando sobre las salidas con valor de "1" la salida Boleana del circuito está dada en función de sus minterms por la siguiente expresión:

Salida = A·B·C + ABC + ABC + ABC + ABC

El mapa de Karnaugh que corresponde a esta expresión es el siguiente:

PROBLEMA: Dibujar los mapas de Karnaugh para las siguientes expresiones:

__1) AB + A·B·C + BC

__2) ABC + B + BC

Puesto que ambas expresiones están dadas como sumas-de-productos, la representación apropiada en ambos casos es a través de minterms. Los mapas deseados tendrán el siguiente aspecto:

1)

2)

PROBLEMA: Representar en un mapa de Karnaugh la siguiente expresión:

ABCD + AB·C·D + ABD + A·B·CD + A·C

El mapa de Karnaugh para esta expresión Boleana de cuatro variables es el siguiente:

PROBLEMA: Una configuración produce la siguiente salida:

f = AB + ABCD + A·B·CD + A·B·D + A·B·CD

Simplificar la configuración utilizando el mapa de Karnaugh.

El mapa de Karnaugh, mostrando un posible agrupamiento simplificador, es el siguiente:

Según se puede observar en el mapa, una primera simplificación se puede llevar a cabo enrollando el mapa horizontalmente alrededor de un cilindro para que varios cuadros queden cubiertos por la expresión B·C. Sin embargo, esto deja fuera tres "unos". Buscamos a continuación la mejor manera de agrupar los "unos" restantes como se muestra en el siguiente agrupamiento:

Estos dos agrupamientos "cobijan" todos los "unos"faltantes. Vemos que los demás "unos" se pueden agrupar bajo las expresiones AB y B·D. La salida simplificada estará dada entonces por la siguiente relación:

f = AB + B·C + B·D

PROBLEMA: Utilizando el mapa de Karnaugh, simplificar la siguiente expresión:

f = ABCD + ABCD + ABC·D + AB·CD + ABCD + ABCD + A·B·CD + A·B·CD

El mapa de Karnaugh correspondiente a esta expresión, con una posible simplificación, es el siguiente:

La solución posible indicada en el mapa resulta ser:

f = ABD + ACD + ABC + A·BD

Existe, sin embargo, otra solución posible, la cual se indica en el siguiente mapa de Karnaugh (uno de los agrupamientos se obtiene enrollando el mapa horizontalmente uniendo el borde derecho con el borde izquierdo):

Vemos pues que la solución alterna está dada por la relación:

f = ABC + BCD + ACD + B·CD

En este problema, el mapa de Karnaugh nos proporciona dos soluciones diferentes para un mismo caso, cualquiera de las cuales es igualmente aceptable y válida. Corresponderá al ingeniero de diseño decidir cuál de las dos soluciones es más económica de construír con los componentes que tenga disponibles a la mano.

PROBLEMA: Representar en mapas de Karnaugh las siguientes expresiones que contienen maxterms:

1) (A + B) ∙ (A + B + C) ∙ (A + B + C + D) ∙ (B + C + D)

2) (A + B + C) ∙ (A + C + D) ∙ (B + C + D) ∙ (A + D)

Los mapas de Karnaugh pedidos son los siguientes:

1)

2)

PROBLEMA: Un circuito produce la siguiente Tabla de Verdad. Usando maxterms, encontrar su salida y simplificar dicha expresión usando el mapa de Karnaugh:

Usando maxterms, la salida del circuito está dada por la siguiente relación:

(A + B + C + D) ∙ (A + B + C + D) ∙ (A + B + C + D) ∙ (A + B + C + D) ∙ (A + B + C + D)

El mapa de Karnaugh con las agrupaciones simplificadoras posibles es el siguiente:

Del mapa vemos que la expresión de salida simplificada será:

Salida = (B + C + D) ∙ (A + C + D) ∙ (A + B +D) ∙ (A + B + C)

PROBLEMA: Se requiere construír un circuito lógico que produzca las siguientes salidas:

Haciendo uso del mapa de Karnaugh y diseñando alrededor de los minterms, encontrar un circuito minimizado que pueda producir las salidas deseadas.

Lo primero que debemos notar es que aunque se trata de un circuito lógico de cuatro variables, no todas las 16 combinaciones posibles de variables están presentes, tales como las combinaciones ABCD=1110, ABCD=1101, etc., lo cual podemos tomar como un indicativo de que tales combinaciones no están presentes por el simple hecho de que no serán utilizadas para los propósitos que persigue el circuito lógico que está siendo diseñado. En otras palabras, son combinaciones redundantes, las cuales no importa que tomen un valor de "1" ó de "0". Y si son redundantes, las podemos meter dentro del mapa de Karnaugh simbolizadas con una "X", dando a entender con esto que pueden tomar un valor de "1" ó de "0" sin que ello afecte en lo absoluto los requerimientos finales del diseño. El mapa de Karnaugh del circuito, mostrando las simplificaciones posibles que se pueden lograr aprovechando las combinaciones redundantes, es el siguiente:

Enmarcados en un recuadro de color verde, los minterms AB·CD y AB·C·D junto con las redundancias ABC·D, ABCD, ABCD, ABCD, ABCD y ABCD se reducen a la variable A. Enmarcados en un recuadro de color rojo, los minterms ABCD y ABCD junto con las redundancias ABCD y ABCD se reducen al término BC. Y enmarcados en un recuadro de color azul, los minterms A'BCD y A'BC'D junto con las redundancias ABCD y ABCD se reducen al término BD. La salida del circuito minimizado resulta ser entonces:

Salida = A + BC + BD

PROBLEMA: Escribir, mostrando todas las variables Boleanas en forma explícita, las expresiones representadas por la siguiente notación compacta:

(1) F(a,b,c) = Σm(0,2,7)

(2) F(A,B,C,D) = Σm(0,1,3,4,5,7,12,13,15)

(3) F(A,B,C,D) = Σm(15,11,7,14,10,12,6,4)

(4) Z = Σm(0,1,2,4,6)

En el primer caso que involucra a tres variables, la expresión Boleana explícita será:

F(a,b,c) = Σm(000,010,111)

F(a,b,c) = a∙b∙c + abc + abc

En el segundo caso, la expresión Boleana explícita será:

F(A,B,C,D) = Σm(0000,0001,0011,0100,0101,0111,1100,1101,1111)

F(A,B,C,D) = A∙B∙C∙D + A∙B∙CD + A∙BCD + ABC∙D + ABCD

+ ABCD + ABC∙D + ABCD + ABCD

En el tercer caso, la expresión Boleana explícita será:

F(A,B,C,D) = Σm(1111,0111,1110,1010,1100,0110,0100)

F(A,B,C,D) = ABCD + ABCD + ABCD + ABCD + ABC∙D + ABCDD + ABC∙D

Y en el cuarto caso que podemos suponer que involucra a tres variables puesto que el decimal más grande de todos no excede de 7 (111), designando a dichas variables como p, q y r la expresión Boleana explícita será:

Z = Σm(000,001,010,100,110)

Z = p∙q∙r+ p∙q + pqr + pq∙r + pqr

PROBLEMA: Mediante el método de Quine-McCluskey, simplificar la siguiente expresión.

Z = A∙B∙C + A∙B∙C + AB∙C + ABC

Usaremos la notación compacta para simplificar los listados que se llevarán a cabo, con la cual:

Z = Σ(000,001,100,101)

Z = Σm(0,1,4,5)

Agrupando los términos según sus índices, podemos llevar a cabo una simplificación sucesiva pasando de una primera lista a una segunda lista y tras esto a una tercera lista de la manera mostrada:

En la segunda lista podemos ver que la expresión original ha sido reducida a:

Z = A∙B + B∙C + BC + AB

Y en la tercera lista vemos que la expresión final simplificada es Z=B.

En este caso, dada la simplicidad de la minimización, no fue necesario trazar ninguna retícula.

PROBLEMA: Mediante el método de Quine-McCluskey, simplificar la siguiente expresión.

Z = A∙B∙CD + A∙BCD + ABCD + ABCD' + ABCD + ABCD' + A∙BCD

Por comodidad, usaremos la notación compacta para simplificar los listados que se llevarán a cabo, con lo cual:

Z = Σm(0000,0010,0100,0101,1000,1001,1100)

Z = Σm(0,2,4,5,8,9,12)

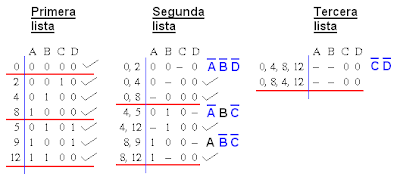
Agrupando los términos según sus índices, podemos llevar a cabo una simplificación sucesiva pasando de una primera lista a una segunda lista y tras esto a una tercera lista de la manera mostrada:

De la simplificación sucesiva podemos ver que los implicantes primarios de la expresión Boleana original son A∙B∙D, ABC, AB∙C y C∙D.

Finalmente, y aunque no es indispensable en este problema, construímos una retícula con la finalidad de confirmar que ninguno de los implicantes primarios obtenidos es redundante:

Podemos ver que la solución final de la minimización es entonces:

Z = A∙B∙D + ABC + AB∙C + C∙D

PROBLEMA: Mediante el método de Quine-McCluskey, simplificar la siguiente expresión.

Z = A∙B∙C∙D + A∙B∙CD + A∙BCD + A∙BCD + ABCD + ABCD

+ AB∙C∙D + ABCD + ABC∙D + ABCD + ABCD

Nuevamente, por comodidad usaremos la notación compacta para simplificar los listados que se llevarán a cabo, con lo cual:

Z = Σm(0000,0001,0010,0011,0101,0111,1000,1010,1100,1101,1111)

Z = Σm(0,1,2,3,5,7,8,10,12,13,15)

Agrupando los términos según sus índices, podemos llevar a cabo una simplificación sucesiva pasando de una primera lista a una segunda lista y tras esto a una tercera lista de la manera mostrada:

De la simplificación sucesiva podemos ver que los implicantes primarios de la expresión Boleana original son A∙B, B∙D, AD, BD, AC∙D y ABC. Finalmente, construímos una retícula con la finalidad de remover a los implicantes primarios redundantes:

Podemos ver que la solución final de la minimización, con los implicantes primarios redundantes ya removidos, es entonces:

Z = B∙D + BD + A∙B + AC∙D

PROBLEMA: Mediante el método de Quine-McCluskey, simplificar la siguiente expresión.

Z = A∙B∙C∙D + A∙B∙CD + A∙BCD + A∙BCD + ABC∙D + ABCD

+ ABCD + AB∙CD' + AB∙CD + ABCD + ABCD

Agrupando los términos según sus índices, podemos llevar a cabo una simplificación sucesiva pasando de la primera lista que aparece en el extremo izquierdo a la segunda lista en donde puede apreciarse que los términos de cuatro variables han sido reducidos a términos de tres variables, pasando finalmente a la tercera lista en el extremo derecho en la cual los términos de tres variables han sido reducidos a términos de dos variables:

Finalmente, construímos la retícula en la cual "graficamos" los implicantes primarios obtenidos en su relación con los minterms de la expresión original:

De la reticula podemos ver que la expresión final simplificada es:

Z = B∙C + A∙D + CD

El método de Quine-McCluskey es superior al mapa de Karnaugh en el sentido de que el primero se presta a ser programado para ser resuelto de manera automática por una computadora. Repasando los problemas anteriores, cualquiera que tenga conocimientos previos en programación en algún lenguaje como BASIC ó C++ podrá ir formando ya en su mente un algoritmo ("receta de cocina" generalizada especificando una serie de pasos para la resolución de un problema computacional) para llevar a cabo la minimización de un circuito lógico en forma automatizada mediante el método Quine-McCluskey, el cual siempre garantiza la obtención de la configuración mínima. Sin embargo, el principal problema con el método de Quine-McCluskey, visible ya para alguien con conocimientos de programación que quiera elaborar su programa para generalizar el método hacia cualquier número de variables, es que tiene que llevar a cabo una búsqueda exhaustiva agotando una por una todas las posibilidades, lo cual en la materia clásica de Estructuras de Datos equivale a tener que recorrer todos los nodos de un "árbol" que se va formando al irse acumulando los resultados parciales obtenidos en la búsqueda de la solución óptima. Esto, desde luego, pone al método de Quine-McCluskey dentro de una categoría de problemas matemáticos conocidos como NP-"duros", lo cual en términos llanos significa que el algoritmo de Quine-McCluskey va creciendo exponencialmente de acuerdo a la cantidad de variables de entrada aumentando enormemente la cantidad de tiempo computacional requerido a medida que aumenta la cantidad de entradas a un circuito lógico, lo cual eventualmente limita el rango de aplicación del método.

PROBLEMA: Así como hay una notación compacta para representar una expresión Boleana puesta en función de sus minterms como una suma de productos, también hay una notación compacta para representar una expresión Boleana puesta en función de sus maxterms como un producto de sumas. Bajo esta notación, la siguiente expresión Boleana escrita empleando maxterms, como un producto de sumas:

Salida = (A + B + C)(A + B + C)

puede ser convertida a notación compacta recordando la manera en la cual se definen los maxterms a partir de una Tabla de Verdad (recuérdese que en un maxterm la suma Boleana de las variables debe ser siempre cero, debiéndose complementar aquellas variables que sean "1" para que así haya únicamente "ceros" en la formación del maxterm). Así, la expresión dada arriba queda representada en forma compacta de la siguiente manera:

Salida = ΠM(000,001)

o bien, usando la más familiar notación decimal:

Salida = ΠM(0,1)

Revirtiendo los pasos, podemos reconstruír la expresión original. Obsérvese que se ha utilizado la letra griega Pi mayúscula (Π) para indicar que se trata de un producto de sumas. El par "ΠM" se lee como "el producto de maxterms".

Definido lo anterior, representar en forma compacta las siguientes expresiones:

(1) F(A,B,C) = (A + B + C) ∙ (A + B + C)

(2) F(A,B,C,D) = (A+B+C+D) ∙ (A+B+C+D) ∙ (A+B+C+D) ∙ (A+B+C+D)

(2) Z = (A+B+C+D) ∙ (A+B+C+D) ∙ (A+B+C+D) ∙ (A+B+C+D) ∙ (A+B+C+D)
__________∙ (A+B+C+D) ∙ (A+B+C+D)

Para la primera expresión, convirtiendo cada maxterm a su equivalente binario de acuerdo con la combinación de "unos" y "ceros" que lo producirían en una Tabla de Verdad:

F(A,B,C) = ΠM(101,110)

F(A,B,C) = ΠM(5,6)

Para la segunda expresión, convirtiendo cada maxterm a su equivalente binario de acuerdo con lo que lo produciría en una Tabla de Verdad:

F(A,B,C,D) = ΠM(0101,1000,0011,1001)

F(A,B,C,D) = ΠM(5,8,3,9)

Reacomodando:

F(A,B,C,D) = ΠM(3,5,8,9)

Para la tercera expresión, convirtiendo cada maxterm a su equivalente binario de acuerdo con lo que lo produciría en una Tabla de Verdad:

Z = ΠM(0010,0110,1110,1010,1000,1001,1011)

Z = ΠM(2,6,14,10,8,9,11)

Reacomodando:

Z = ΠM(2,6,8,9,10,11,14)

PROBLEMA: Encontrar, para un circuito de dos salidas con cuatro variables de entrada, cuyos mapas de Karnaugh sean los siguientes:

los agrupamientos comunes que podrían ser utilizados para formar sub-circuitos comunes reduciendo con ello la cantidad de componentes y alambrado requerido.

Con ambos mapas de Karnaugh puestos lado a lado, podemos captar de inmediato las siguientes tres regiones comunes (una encerrada en una línea roja, la otra en una línea verde, y la otra en una línea azul) que podrían ser utilizadas para formar sub-circuitos:

Obsérvese que no estamos utilizando aquí el mapa de Karnaugh en su sentido "clásico" para minimizar una función Boleana dentro del mapa, sino para detectar las regiones comunes en mapas diferentes. Sin embargo, una vez detectadas las regiones comunes a mapas diferentes, podemos tratar de minimizar dichas regiones comunes dentro de cada mapa (la simplificación en todo caso será la misma para regiones iguales). Esta técnica se puede extender a circuitos lógicos con tres, cuatro, cinco o más salidas. El inconveniente de ir extendiendo este método a una cantidad mayor de variables de salida es que con muchos mapas de Karnaugh puede ir resultando más difícil captar las regiones comunes.