3A: Problemas resueltos

PROBLEMA: ¿Cuál es la salida de los siguientes componentes y circuitos en términos del álgebra Boleana?

(1) Para el bloque AND con cuatro terminales de entrada, extendemos la definición Boleana del bloque AND de dos terminales de entrada en el cual la salida de un AND que tenga dos entradas A y B estará dada por el producto Boleano de dichas variables de entrada, o sea AB. Del mismo modo, la salida de un AND que tenga cuatro entradas A, B, C y D estará dada también por el producto Boleano de dichas variables de entrada: la salida del AND será entonces ABCD.

(2) Para el bloque OR con cuatro terminales de entrada, extendemos la definición Boleana del bloque OR de dos terminales de entrada en el cual la salida de un OR que tenga dos entradas A y B estará dada por la suma Boleana de dichas variables de entrada, o sea A+B. Del mismo modo, la salida de un OR que tenga cuatro entradas A, B, C y D estará dada también por la suma Boleana de dichas variables de entrada. La salida del AND será entonces A+B+C+D.

(3) Analizando el diagrama del circuito, vemos que la salida del AND superior será igual al producto de las variables de entrada A y B, o sea AB, mientras que la salida del AND inferior será igual al producto de las variables de entra C y D, o sea CD. Como estas salidas son alimentadas a un OR en donde son sumadas, la salida del OR será entonces AB+CD.

(4) Analizando el diagrama, tenemos una situación parecida al circuito anterior, excepto que la salida de cada AND es invertida antes de ser introducida al OR. Esto quiere decir que, del primer AND, el OR recibirá como entrada A·B, mientras que del segundo AND el OR recibirá como entrada C·D. Estas dos entradas son sumadas en el OR, produciendo a la salida del mismo A·B+C·D.

PROBLEMA: En ciertos textos, sobre todo algunos utilizados para introducir no a los ingenieros y técnicos sino a los estudiantes de las ciencias puras (especialmente aquellos que cursan las Licenciaturas de Matemáticas), es frecuente abrir el tema del álgebra Boleana con una representación en la cual las funciones OR y AND se llevan a cabo mediante simples interruptores eléctricos. Bajo esta representación, la acción de un circuito OR que ocurre en un circuito sencillo como el siguiente (ampliar imagen para ver la acción animada en caso de no haber animación visible):

es representada simbólicamente de la siguiente manera:

y la acción de un circuito AND que ocurre en un circuito sencillo como el siguiente (ampliar imagen para ver la acción animada en caso de no haber animación visible):

es representada simbólicamente de la siguiente manera:

Bajo esta representación, ¿cuál será la ecuación Boleana del siguiente circuito?

¿Qué desventaja puede tener en la práctica este tipo de interpretación lógica?

En el circuito proporcionado, los interruptores q y p están en serie, en una combinación AND, y su equivalente Boleano es pq. Y como esto está en paralelo con el interruptor s, esta parte del circuito tiene una representación Boleana pq+s. Y como esto está en serie con otro interruptor s, la representación Boleana de la parte superior de la red es s(pq+s). La parte inferior de la red son tres interruptores q, r y p en serie, en una combinación AND cuyo equivalente Boleano es pqr. Y como la parte superior del circuito cuya representación Boleana es pq+s está en paralelo con la parte inferior del circuito cuya representación Boleana es pqr, el equivalente Boleano del circuito es:

s(pq + s) + pqr

La principal desventaja en la práctica de este tipo de interpretación lógica es que no existe el inversor lógico, no existe la función NOT, y esta función no se puede implementar simplemente con interruptores eléctricos como los aquí mostrados.

PROBLEMA: ¿Cuál es la salida Boleana del siguiente circuito?

Un AND forma el producto AB y el otro forma el producto CD. Ambos términos son sumados (suma Boleana) en el bloque NOR, el cual además de sumarlos los complementa, dando como resultado AB + CD, lo cual entra al NOR inferior, el cual a su vez por tener un "0" (simbolizado como "tierra eléctrica") en una de sus entradas actúa como un simple inversor, complementando a un complemento con lo cual se cancela la acción de ambos, dejando como salida A+B. Trazando las señales a través de las funciones lógicas todo esto equivale a:

PROBLEMA: ¿Cuál es la salida del siguiente circuito? Escribir además una Tabla de Verdad para el mismo.

Trazando las señales a través de las funciones lógicas, obtenemos lo siguiente:

Podemos ver que la salida del circuito a través de la función AND en el extremo derecho estará dada por la siguiente expresión:

[A(A + B)][AB + A + B]

La Tabla de Verdad se puede obtener sustituyendo en la expresión anterior todas las combinaciones posibles de "unos" y "ceros" en las literales A y B y evaluando la salida para cada combinación en particular. Por ejemplo, para la combinación A=0 y B= 0:

[A(A + B)][AB + A + B] = [0(0 + 0)][0 • 0 + 0 + 0]

= [1(1 + 0)][0 + 1 + 0]

= [1(1)][1] = [1][1] = 1

De este modo, la Tabla de Verdad obtenida será como se muestra a continuación:

PROBLEMA: ¿Cuál es la salida del siguiente circuito? Escribir además una Tabla de Verdad para el mismo.

Trazando las señales a través de las funciones, se tiene lo siguiente:

La salida es:

Considerando todas las combinaciones posibles de "unos" y "ceros", la Tabla de Verdad para la salida del OR de tres entradas es como se muestra a continuación:

PROBLEMA: ¿Cuál es la salida Boleana del siguiente circuito lógico?

Veamos primero cuál es la salida Boleana del primer AND de tres entradas (el que está puesto más arriba en el diagrama). Este AND tiene una primera entrada B, tiene una segunda entrada C y tiene una tercera entrada D. Entonces la salida Boleana de este AND será BCD. Ahora veamos cuál es la salida Boleana del segundo AND de dos entradas. Este AND tiene una entrada A y tiene otra entrada D, con lo cual su salida Boleana será AD. El tercer AND de tres entradas tiene una primera entrada B, tiene una segunda entrada C, y tiene una tercera entrada D. Entonces su salida Boleana será BCD. Por último, el cuarto AND de tres entradas tiene una primera entrada A, tiene una segunda entrada B, y tiene una tercera entrada C, con lo cual su salida Boleana será A·B·C. Puesto que las salidas de los cuatro ANDs es sumada (en el sentido Boleano) por el bloque OR, la salida F estará dada por la expresión:

F= BCD + AD + BCD + A·B·C

PROBLEMA: Se nos asegura que un circuito de dos entradas tiene una salida AB+A·B. ¿Cuál es el diagrama de tal circuito?

El hecho de que el resultado final sea la suma de dos cantidades nos indica que hay una función OR al final, dando:

La cantidad AB es un producto Boleano obtenido en una función AND, dando así:

Asimismo, con la otra expresión:

Los términos de la expresión inferior a la entrada de la misma se pueden obtener invirtiendo las señales de entrada a través de la función NOT, esto es:

Uniendo las señales que tienen el mismo punto de origen tenemos el diagrama final del circuito completo:

PROBLEMA: Dado un circuito cuya salida es

AB + CD

¿cuál es el diagrama del circuito que corresponde a dicha expresión Boleana (no es necesario simplificar la expresión)?

Usando el mismo razonamiento que en el problema anterior, trabajando hacia atrás usando la expresión de salida como punto de referencia, tenemos primeramente que toda la expresión es una expresión invertida lógicamente, o sea que ha pasado por un NOT inversor:

La expresión antes de ser invertida por el NOT es AB+CD., lo cual quiere decir que hay un OR uniendo los productos Boleanos con que está siendo alimentado. A continuación tenemos el diagrama cumulativo del circuito:

Y por último, agregando los bloques AND con los cuales las variables de entrada A y B así como las variables de entrada C y D están siendo multiplicadas respectivamente, tenemos el diagrama completo del circuito:

Esta es una configuración famosa conocida como la configuración AOI (And-Or-Invert) porque la primera operación que efectúa sobre las entradas es la operación AND, la siguiente operación es la operación OR y la última operación es la operación de INVERSION. Obsérvese que si conectamos las terminales C y D entre sí mandando la terminal resultante a la condición "cero" (esto es, poniendo un "0" lógico en ambas) tendremos entonces una función NAND de entradas A yB. Por otro lado, si conectamos las terminales A y B entre sí designando a la terminal resultante como X, y conectamos las terminales C y D entre sí designando a la terminal resultante como Y, tendremos entonces una función NOR de entradas X y Y. Y si conectamos todas las terminales de entrada A, B, C y D entre sí formando una sola terminal de entrada, tendremos entonces la función NOT.

La habilidad de la configuración AOI para generar todas estas funciones lógicas y su facilidad de construcción una vez estandarizada son las razones principales de la popularidad que ha tenido esta configuración en los estudios teóricos llevados a cabo en los círculos académicos, aunque en la práctica la configuración AOI no es tan útil como pudiera serlo en virtud de que se puede demostrar que todas las funciones lógicas básicas se pueden generar a partir del bloque NAND, o bien a partir del bloque NOR, precisamente los componentes básicos en la construcción de estas funciones bajo varias familias lógicas (para mayores detalles sobre esto, véase el Suplemento # 1 a esta obra).

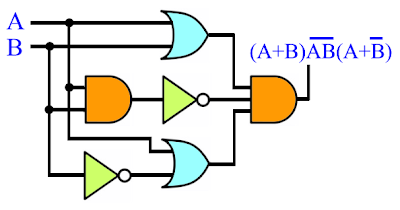
PROBLEMA: La salida producida por un circuito es (A+B)·(A · B)·(A+B). Sin simplificar la expresión mediante álgebra Boleana, ¿cuál es su diagrama equivalente?

Trabajando "hacia atrás", descomponiendo la información a la salida en sus partes esenciales, tenemos la siguiente secuencia de pasos, los cuales no serán explicados con palabras porque el procedimiento visual por sí solo será bastante claro:

El diagrama final resulta ser el siguiente:

PROBLEMA: Dadas las secuencias A=011001 y B=110100, calcular:

(1) A + B y A · B


(2) A · B y A + B

¿Qué se puede deducir de los resultados?

(1) Si A=011001, entonces A=100110. Y si B=110100, entonces B=001011.

En base a esto, la suma Boleana será:

A + B = 111101

de lo cual se deduce que:

A + B = 00010

Por otro lado, el producto Boleano de los complementos es:

A · B = 00010

Inspeccionando las dos palabras binarias A y B, resulta claro que al aparearlas bit por bit las dos contienen todas las combinaciones posibles de "unos" y "ceros" al ser combinadas (A=0 y B=0, A=0 y B=1, A=1 y B=0, A=1 y B=1).

Comparando los resultados obtenidos, se concluye que:

A + B = A · B

En notación alterna: (A+B)' = A' · B'

(2) De las palabras dadas obtenemos el siguiente producto Boleano de las mismas:

A·B = 010000

de lo cual se deduce que:

A · B = 101111

Por otro lado, la suma de los complementos es:

A + B = 101111

Comparando los resultados obtenidos, se concluye que:

A · B = A + B

En notación alterna: (A · B)' = A' + B'

Las relaciones obtenidas son mejor conocidas como las leyes de DeMorgan, en honor al logista Augustus DeMorgan (1806-1871) quien fué quien las descubrió por vez primera. Pero al igual que Boole, el inventor del álgebra Boleana, DeMorgan jamás se imaginó que su descubrimiento pudiera tener aplicación alguna en el estudio de los circuitos digitales. En combinación con el álgebra Boleana, estas dos relaciones son extraordinariamente importantes en la simplificación de expresiones que corresponden a circuitos lógicos. Estas leyes son generalmente presentadas de la siguiente manera en otros libros de texto:

A + B = A · B :

El complemento de una suma de variables es igual al producto de los complementos.

A · B = A + B :

El complemento del producto de dos variables es igual a la suma de los complementos.

Como lo sugieren estos enunciados, las leyes de DeMorgan se pueden extender hacia tres o más variables sin dificultad alguna. La demostración formal de este hecho es relativamente fácil recurriendo a un procedimiento conocido como la inducción matemática. Por curiosa coincidencia, fue precisamente Augustus DeMorgan quien formalizó el término y el concepto de la inducción matemática.

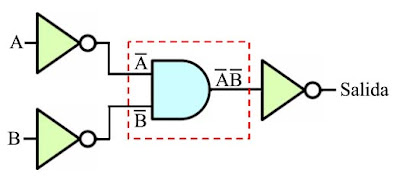
PROBLEMA: ¿Cuál es la salida del siguiente circuito? (Obsérvese que todas las entradas están complementadas)

De un AND sale el producto A·B, mientras que del otro AND sale el producto C·D. Ambos productos entran al NOR, el cual podemos considerar que primero lleva a cabo la suma Boleana OR produciendo A·B+C·D, e inmediatamente lleva a cabo la inversión de esto, complementando todo. Aplicando los teoremas de DeMorgan a la expresión resultante, podemos ver que con los siguientes pasos:

la salida resultante es igual a A+B, lo cual podemos adjuntar al diagrama en el rastreo del flujo de señales:

PROBLEMA: Un principio aparentemente obvio es el siguiente: "Si las entradas a un elemento lógico se invierten (inversión lógica con bloques NOT) y la salida del elemento también se invierte, se obtiene entonces la misma acción que la que se obtendría del elemento sin la presencia de los inversores". Comprobar la veracidad de este enunciando usando un bloque AND como punto de partida.

Un bloque AND de dos entradas con inversores puestos tanto a las entradas como a la salida presentará el siguiente aspecto:

La salida de este circuito lógico estará dada por:

Para la simplificación Boleana, en la segunda línea, aplicamos una de las Leyes de DeMorgan, mientras que para pasar de la segunda línea a la tercera línea aplicamos el teorema que nos dice que la inversión de una inversión cancela los efectos de ambas sobre la variable en la cual operan.

Puesto que la salida es ahora la correspondiente a un bloque OR y no la correspondiente a la del bloque AND que teníamos originalmente, se concluye que el enunciado propuesto es falso. La misma conclusión se podría haber obtenido si se hubiese usado un bloque OR para comprobar lo propuesto.

PROBLEMA: En la familia lógica de circuitos conocida como RTL (Resistor Transistor Logic, véase el Suplemento # 1 para mayores detalles) el bloque fundamental es la función NOR. Obtener usando esta función como punto de partida las tres funciones lógicas básicas NOT, OR y AND.

Conectando todas las terminales de entrada de un NOR entre sí se puede obtener la función NOT:

NOT

Invirtiendo la salida de un NOR con un NOT así obtenido se puede lograr fácilmente la función OR:

OR

Por último, para obtener la función AND usando bloques NOR hay que relacionarla de alguna manera con la suma Boleana propia de la función NOR usando para ello una de las relaciones de DeMorgan. Buscamos dicha relación trabajando "a la inversa" (llevando a cabo pasos opuestos a los que normalmente tomaríamos para simplificar una expresión):

Vemos que basta invertir las entradas de un NOR para convertirlo en un AND. Por lo tanto, el circuito deseado es el siguiente:

AND

Si queremos, podemos obtener fácilmente la función NAND invirtiendo la salida de este AND con el NOT obtenido previamente a base de bloques NOR.

Puesto que, a partir de bloques NOR exclusivamente, podemos recuperar las tres funciones lógicas básicas, al bloque NOR se le conoce también como una función universal.

PROBLEMA: En la familia lógica de circuitos conocida como TTL (Transistor Transistor Logic, véase el Suplemento # 1 para mayores detalles) el bloque fundamental es la función NAND. Obtener usando esta función como punto de partida las tres funciones lógicas básicas NOT, OR y AND.

Al igual que en el problema anterior, conectando todas las terminales de entrada de un NAND entre sí se puede obtener la función NOT:

NOT

Invirtiendo la salida de un NAND con un NOT así obtenido se puede lograr fácilmente la función AND:

AND

Por último, para obtener la función OR usando bloques NAND hay que relacionarla de alguna manera con el producto Boleano propio de la función NAND usando para ello una de las relaciones de DeMorgan. Buscamos dicha relación trabajando "a la inversa" (llevando a cabo pasos opuestos a los que normalmente tomaríamos para simplificar una expresión):

Vemos que basta invertir las entradas de un NAND para que este se convertierta en un OR. Por lo tanto, el circuito deseado es el siguiente:

OR

Puesto que, a partir de bloques NAND exclusivamente, podemos recuperar las tres funciones lógicas básicas, también al bloque NAND se le conoce también como una función universal.

PROBLEMA: Determinar si es más económico construír el siguiente circuito con bloques NOR o con bloques NAND. Usar los resultados de los dos problemas anteriores.

Este problema es representativo de una situación que ocurre frecuentemente en la práctica. En las familias de componente electrónicos utilizados para construír circuitos lógicos, es muy rara la ocasión (como lo es el caso de los relevadores electromecánicos) en la cual por la naturaleza propia del funcionamiento intrínseco de la familia los componente más sencillos no son el AND y el OR sino el NAND o el NOR, existiendo frecuentemente la opción de poder seleccionar entre estos dos últimos para construír un circuito lógico. Y también, con mucha frecuencia, habrá una diferencia en la cantidad de componentes requeridos al usar el bloque NOR y al usar el bloque NAND, lo cual puede constituírse en una razón para preferir un tipo de bloque sobre el otro. Y la razón principal no es ya tanto el factor costo, ya que el lograr que un diseño utilice 14 componentes en lugar de 16 no representa ya en estos tiempos un ahorro substancial de dinero; la razón principal es hoy la velocidad máxima bajo la cual puede funcionar un circuito lógico, entre menor sea la cantidad de componentes utilizados, menor será el tiempo que tarda una señal en llegar de un punto a otro dentro del circuito.

Comenzaremos el rediseño utilizando primero bloques NAND. Para ello, simplificaremos la representación del inversor NOT construído mediante un bloque NAND con sus dos entradas conectadas a un mismo punto. La representación esquemática es la siguiente:

Es importante tener siempre en mente que el bloque de la derecha no es un NAND de una sola entrada, todo NAND debe tener por lo menos dos entradas; se trata de un NAND que está actuando como un inversor lógico NOT por tener sus dos entradas conectadas a un mismo punto. Esto permite dar mayor claridad a los diagramas y es una práctica justificada en el trazado de los diagramas esquemáticos.

Usando únicamente bloques NAND y los resultados de uno de los problemas anteriores, el circuito toma el siguiente aspecto:

Del diagrama, podemos ver que el circuito se puede simplificar. Puesto que dos NOTs conectados en serie no alteran la señal a su entrada (debido a que el inverso del inverso de una variable Boleana es igual a la variable misma, o sea (A')' = A), estos se pueden reemplazar por una sola línea directa. Se han destacado dos de ellos de color rosa. Hay otros dos que se pueden eliminar en la parte inferior. De este modo, el circuito toma el siguiente aspecto:

Vemos que la construcción del circuito con bloques NAND requiere un mínimo de 5 bloques NAND.

Procedemos ahora a construír el circuito utilizando para ello bloques NOR. Así como simplificamos los esquemáticos utilizando un NAND de "una sola entrada", utilizaremos un NOR de "una sola entrada" actuando como inversor NOT, el cual se sobreentiende que ha derivado de un NOR de dos entradas con ambas entradas conectadas:

Usando únicamente bloques NOR y los resultados de uno de los problemas anteriores, el circuito toma el siguiente aspecto:

Del diagrama, podemos ver que el circuito se puede simplificar por las mismas razones expuestas en la simplificación anterior debido a que dos NOTs conectados en serie no alteran la señal a su entrada y se pueden reemplazar por una sola línea directa. En el diagrama se han destacado dos de ellos de color rosa. Hay otros dos en el circuito que también se pueden eliminar. De este modo, el circuito toma el siguiente aspecto:

Vemos que la construcción del circuito con bloques NOR requiere un mínimo de 6 bloques NOR. Puesto que se requiere un número menor (5) de bloques NAND que de bloques NOR (6) para construír el circuito propuesto, concluímos que es más económico construír el circuito con bloques NAND.

PROBLEMA: Demostrar los siguientes nueve teoremas básicos del álgebra Boleana:

(1) A + 1 = 1

(2) A • 1 = A

(3) A + 0 = A

(4) A • 0 = 0

(5) A + A = A

(6) A • A = A

(7) ā = a

(8) A + A = 1

(9) A • A = 0

(1) Para llevar a cabo la demostración, consideramos los dos valores posibles que puede tomar la variable Boleana A, los cuales son 0 y 1:

A + 1 = 0 + 1 = 1

A+ 1 = 1 + 1 = 1

En ambos casos, obtenemos siempre 1. Se concluye que A + 1 = 1.

(2) Considerando los dos valores posibles, 0 y 1:

A • 1 = 0 • 1 = 0 = A

A • 1 = 1 • 1 = 1 = A

En ambos casos, recuperamos el valor original de A. Se concluye que A • 1 = A.

(3) Considerando los dos valores posibles, 0 y 1:

A + 0 = 0 + 0 = 0 = A

A + 1 = 1 + 0 = 1 = A

En ambos casos, recuperamos el valor original de A. Se concluye que A + 0 = A.

(4) Considerando los dos valores posibles, 0 y 1:

A • 0 = 0 • 0 = 0

A • 0 = 1 • 0 = 0

En ambos casos, obtenemos siempre 0. Se concluye que A • 0 = 0.

(5) Considerando los dos valores posibles, 0 y 1:

A + A = 0 + 0 = 0 = A

A + A = 1 + 1 = 1 = A

En ambos casos, recuperamos el valor original de A. Se concluye que A + A = A.

(6) Considerando los dos valores posibles, 0 y 1:

A • A = 0 • 0 = 0 = A

A • A = 1 • 1 = 1 = A

En ambos casos, recuperamos el valor original de A. Se concluye que A • A = A.

(7) Considerando los dos valores posibles, 0 y 1, para a=0 la primera inversión lógica de a convierte al 0 en un 1, o sea a'=1, y tras esto la segunda inversión convierte al 1 en el 0 que teníamos, o sea que (a')' = a para a=0. Por otro lado, para a=1 la primera inversión lógica de a convierte al 1 en un 0, o sea a'=0, y tras esto la segunda inversión convierte al 0 en el 1 que teníamos, o sea que (a')' = a para a=1. Siendo válida la operación de doble inversión tanto para a=0 como para a=1, la relación queda demostrada.

(8) Considerando los dos valores posibles, 0 y 1:

A + A = 0 + 1 = 1

A + A = 1 + 0 = 1

En ambos casos, obtenemos siempre 1. Se concluye que A + A = 1.

(9) Considerando los dos valores posibles 0 y 1:

A • A = 0 • 1 = 0

A • A = 1 • 0 = 0

En ambos casos, obtenemos siempre 0. Se concluye que A • A = 0.

PROBLEMA: Simplificar las siguientes expresiones:

1) A + AB

2) AB + AB

3) A(A + B)

4) (A+B)B

5) (A+B)(A+C)

6) (A+B)(A+B)

7) ABC + A·B·C + A·B·C + A·B·C

8) ABC + AC + C

En las simplificaciones de cada expresión se irán aplicando los teoremas que sirvan para la simplificación de las mismas.

1) A + AB = A(1 + B) = A•1 = A

2) AB + AB = A(B + B) = A•1 = A

3) A(A + B) = AA + AB = A + AB = A(1 + B) = A•1 = A

4) (A+B)B = AB + BB = AB + 0 = AB

5) (A+B)(A+C) = AA + AC + BA + BC = A + AC + AB + BC

= A(1 + C) + AB + BC

= A•1 + AB + BC

= A + AB + BC

= A(1 + B) + BC

= A•1 + BC

= A + BC

6) (A+B)(A+B) = AA + AB + BA + BB = A + AB + AB + BB

= A + AB + AB + 0

= A(1 + B) + AB

= A + AB

= A(1 + B)

= A

7) ABC + A·B·C + A·B·C + A·B·C = AB(C + C) + A·C(B + B)

= AB+ A·C

8) ABC + AC + C = ABC + (A + 1)C = ABC + C = (AB + 1)C = C

PROBLEMA: Demostrar que:

A(B + C) = ABC + ABC + ABC

En este problema vamos de una expresión más sencilla a una expresión más compleja en la cual en la expresión final cada término consta de tres factores en lugar de los dos que normalmente produciría la expresión original. Una forma de resolver este problema es trabajar al revés, esto es, tomar la expresión de la derecha y simplificarla para obtener la expresión de la izquierda. Si esto hiciéramos, obtendríamos la siguiente secuencia de pasos que nos llevan de la expresión de la izquierda a la expresión de la derecha:

A(B + C) = AB + AC = AB•1 + AC•1

= AB(C + C) + AC(B + B)

= ABC + ABC + ABC + ABC

= (ABC + ABC) + ABC + ABC

= ABC + ABC + ABC

PROBLEMA: Demostrar que:

AB + AB + AB = A + B

En este caso, lo que se llevará a cabo será efectivamente una simplificación de la expresión en oposición a lo que se hizo en el problema anterior.

AB + AB + AB = AB + AB + AB + AB

= AB + AB + AB + AB

= B(A + A) + A(B + B)

= B + A

= A + B

PROBLEMA: Empezando con la expresión del lado izquierdo de la igualdad de la siguiente relación Boleana, demostrar que:

AB + BC + CA = ABC + ABC + ABC + A·B·C + ABC + A·B·C

y a continuación, usando el mismo principio de solución y empezando con la expresión del lado derecho de la siguiente relación Boleana, demuéstrese que:

AB + BC + CA = AB + BC + CA

Trabajando sobre la expresión del lado izquierdo de la primera relación Boleana proporcionada, tenemos que:

AB + BC + CA = AB•1 + BC•1 + CA•1

= AB•(C + C) + BC•(A + A) + CA•(B + B)

= ABC + AB·C + ABC + + ABC + ABC + A·B·C

= ABC + ABC + ABC + A·B·C + ABC + A·B·C

Siguiendo un procedimiento similar sobre la expresión del lado derecho de la segunda expresión Boleana proporcionada, tenemos que:

AB + BC + CA = AB•1 + BC•1 + CA•1

= AB•(C + C) + BC•(A + A) + CA•(B + B)

= ABC + ABC + ABC + A·B·C + ABC + A·B·C

= ABC + ABC + ABC + A·B·C + ABC + A·B·C

Comparando este último resultado con el anterior, y como sigue siendo válido en álgebra Boleana el principio de que dos cosas iguales a una tercera son iguales entre sí, vemos que:

AB + BC + CA = AB + BC + CA

PROBLEMA: Recurriendo a los resultados del problema anterior, demuéstrese que

(A + B + C) • A · B · C = AB + BC + CA

Podemos comenzar aplicando en el lado izquierdo de la ecuación Boleana el teorema de DeMorgan que nos dice que el complemento del producto de variables es igual a la suma de los complementos de las mismas, con lo cual tenemos:

(A + B + C) • A·B·C = (A + B + C) • (A + B+ C)

Llevando a cabo la multiplicación para remover los paréntesis:

(A + B + C) • A·B·C = AA + AB + AC + AB + BB + BC + AC + BC + CC

Como los productos AA , BB y CC son todos iguales a cero, se cancelan dejando:

= AB + AC + AB + BC + AC + BC

Reagrupando los términos:

= (AB + BC + CA) + (AB + BC + CA)

Puesto que AB+BC+CA=AB+BC+CA de acuerdo con lo obtenido en el problema anterior, se deduce que las cantidades dentro de ambos paréntesis son iguales. Ya que uno de los teoremas Boleanos nos asegura que cantidades iguales sumadas dan la misma cantidad (A+A=A), podemos descartar todo el segundo paréntesis y así obtener:

(A + B + C) • A · B · C = AB + BC + CA

PROBLEMA: Demostrar, recurriendo al uso del álgebra Boleana, que el siguiente circuito no es un circuito útil para el procesamiento de información, por estar su salida "atorada en 1" todo el tiempo:

La salida Boleana de este circuito es igual a la suma Bolena de la entrada b, más el término a · b, siendo este último el producto resultante del pre-procesamiento llevado a cabo por el AND conectado al NOT:

Salida = a · b + b

Aplicando las leyes de DeMorgan, podemos "romper" el primer término en dos términos más sencillos:

Salida = a + b + b

Puesto que de acuerdo a uno de los teoremas ya demostrados, b + b = 1:

Salida = a + 1

Y nuevamente, aplicando otro de los teoremas ya demostrados, tenemos finalmente:

Salida = 1

Este problema es similar a unos que ya vimos en la sección de problemas resueltos correspondiente al Capítulo 2: Las Tres Funciones Lógicas Básicas, en donde también se preguntaba si ciertos circuitos lógicos eran útiles para el procesamiento de información, excepto que en en ese caso, sin el beneficio del álgebra Boleana, se tuvo que recurrir a utilizar todas las combinaciones posibles de "unos" y "ceros" para resolver dichos problemas, mientras que aquí con el álgebra Boleana a nuestra disposición la resolución del problema procede con mucha mayor rapidez.

PROBLEMA: Recurriendo al álgebra Boleana, simplificar el siguiente circuito lo más que se pueda:

El primer paso consiste en obtener la salida Boleana del circuito directamente a partir del diagrama del circuito. La salida del circuito, identificada como y, será igual a la suma Boleana de tres entradas. Una de dichas entradas, la que corresponde al AND superior, está dada por el producto Boleano ab. Otra de dichas entradas, la que corresponde al AND intermedio, está dada por el producto Boleano ab. Y la tercera entrada es la que corresponde al AND inferior, la cual está dada por el producto Boleano a · b. Entonces la expresión Boleana de salida será:

y = a · b + ab + ab

A continuación se presenta la simplificación Boleana de la expresión:

y = a · b + a · (b + b)

y = a · b + a · 1

y = a · b + a

y = a + b

La expresión simplificada nos indica que la terminal c es totalmente irrelevante, puesto que no aparece para nada en la expresión de salida. El circuito simplificado requiere únicamente de un inversor (para invertir lógicamente la entrada b) y de un OR (para sumar a y b).

PROBLEMA: Descríbase la salida del siguiente circuito escribiendo primero en el diagrama las expresiones Boleanas que corresponden a la salida de cada bloque lógico y tras esto la expresión Boleana que este produce, así como su Tabla de Verdad.

Las salidas explícitas de cada bloque son las que se muestran a continuación:

La salida del circuito es AB+AB.

La Tabla de Verdad para este circuito es la que se muestra a continuación:

Estudiando la Tabla de Verdad se observa que la salida es "1" únicamente cuando las dos entradas son diferentes. Este circuito desempeña funciones importantes en el diseño de sistemas digitales, y comúnmente se le designa como OR-EXCLUSIVO, siendo su símbolo el siguiente:

El concepto del OR-EXCLUSIVO se puede extender fácilmente hacia un bloque de esta naturaleza con más de dos entradas, utilizando el mismo principio: la salida será "1" si cualquiera de las entradas es diferente de las demás, y será cero si todas las entradas tienen un valor de "1" ó un valor de "0". Precisamente por esto al OR-EXCLUSIVO se le conoce también como comparador lógico, porque puede comparar dos o mas entradas entradas produciendo una salida de "1" si por lo menos una de las entradas es diferente a las demás.

PROBLEMA: Un diseñista desea utilizar un NOR de 7 entradas cuando cuenta para ello con un bloque NOR de 8 entradas proporcionadas por el circuito integrado CD4078. ¿Qué es lo que se debe de hacer para poder utilizar el NOR de ocho entradas como uno de siete? El mismo diseñista desea utilizar únicamente 3 entradas de un NAND de 4 entradas proporcionadas por el circuito integrado CD4012. ¿Qué es lo que se debe de hacer para poder utilizar el NAND de cuatro entradas como uno de tres?

(1) La salida de un NOR de 8 entradas que llamaremos A, B, C, D, E, F, G y H, cualesquiera que sea la tecnología con la cual haya sido fabricado, está dada por la siguiente expresión:

Salida = A + B + C + D + E+ F +G + H

De esta expresión vemos que basta con poner un "0" permanentemente en cualquiera de las entradas para convertir un NOR de ocho entradas en uno de siete. Por ejemplo, podemos poner un "0" todo el tiempo en la entrada H:

Salida = A + B + C + D + E+ F +G + 0

Salida = A + B + C + D + E+ F +G

(2) La salida de un NAND de 4 entradas A, B, C y D, cualesquiera que sea la tecnología con la cual haya sido fabricado, está dada por la siguiente expresión:

Salida = A · B · C · D

De esta expresión vemos que basta con poner un "1" permanentemente en cualquiera de las entradas para convertir un NAND de cuatro entradas en uno de tres. Por ejemplo, podemos poner un "0" todo el tiempo en la entrada D:

Salida = A · B · C · 1

Salida = A · B · C

Por ningún motivo y bajo ninguna circunstancia se debe dejar terminal de entrada alguna a un circuito lógico sin conexión a ninguna parte. Todas las entradas no utilizadas deben ser conectadas siempre a un "0" ó a un "1" lógico, según sea el caso.

PROBLEMA: Demuéstrese con algebra Boleana que el circuito mostrado a continuación es equivalente a un OR-EXCLUSIVO.

"Rastreando las señales" Boleanas a través del circuito tal y como se llevó a cabo en el problema anterior, tenemos lo siguiente:

La salida del circuito es (A+B)A · B. Aplicando las leyes de DeMorgan podemos llevar a cabo una simplificación mediante el álgebra Boleana:

(A+B)A · B = (A+B)(A + B)

= AA + AB + AB + BB

= AB + AB

en donde las entradas AA y BB se eliminan por uno de los teoremas ya demostrado

Como lo vimos en el problema anterior, esta es la salida de un OR-EXCLUSIVO. Y esto lo pudimos verificar sin necesidad de tener que construír una Tabla de Verdad para el circuito, lo cual evidencia las ventajas de llevar a cabo el análisis mediante el álgebra Boleana.

PROBLEMA: Demostrar que el siguiente circuito es un OR-EXCLUSIVO.

Para resolver el problema, determinamos primero la expresión Boleana producida a la salida del circuito. El OR superior es alimentado con los complementos (inversos) de las variables A y B, o sea con A y B, razón por la cual su salida será A+B. Por su parte, el OR inferior es alimentado directamente con las variables A y B, razón por la cual su salida será A+B. Al ser alimentado el AND con las salidas de los OR, la salida del AND será:

(A+B)(A+B)

Pero esta es la misma expresión intermedia que se obtiene en la resolución del problema anterior, la cual se simplifica a AB + AB. Por lo tanto, el circuito dado es también una implementación de OR-EXCLUSIVO.

PROBLEMA: Como lo vimos en uno de los problemas anteriores, sabiendo que la salida de un OR-EXCLUSIVO de dos entradas puede estar dada por la expresión (A+B)A · B, extender este concepto para encontrar la salida de un OR-EXCLUSIVO de tres entradas A, B y C, poniendo la expresión como una "suma de productos" Boleanos. Constrúyase asimismo una Tabla de Verdad para la expresión obtenida y comprobar así que efectivamente se tiene un OR-EXCLUSIVO de tres entradas. ¿Cuál sería el símbolo para esta función?

Si (A+B)A · B es la salida de un OR-EXCLUSIVO de dos entradas, entonces la salida de un OR-EXCLUSIVO de tres entradas será:

(A+B+C)A · B · C

Simplificando la expresión recurriendo para ello a las leyes de DeMorgan aplicadas a tres variables en vez de dos:

(A+B+C)A · B · C = (A+B+C)(A+B+C)

= AA + AB + AC + BA + BB + BC + CA + CB + CC

= AB + AC + BA + BC + CA + CB

Construyendo a continuación la Tabla de Verdad para todas las combinaciones posibles de "unos" y "ceros", vemos que efectivamente, cuando todas las entradas son iguales la salida es "0", y cuando no son todas iguales entre sí, entonces la salida es "1":

El símbolo usado será el siguiente:

PROBLEMA: ¿Se puede convertir un OR-EXCLUSIVO de tres entradas en un OR-EXCLUSIVO de dos entradas? Justificar la respuesta.

La salida del OR-EXCLUSIVO de tres entradas, según se vió en el problema anterior, está dada por:

Salida = AB + AC + BA + BC + CA + CB

Queremos convertir esto a un circuito cuya salida sea:

Salida = AB + BA

Esto no lo podemos lograr poniendo una de las entradas permanentemente a un "0" lógico, por ejemplo haciendo C=0 en el OR-EXCLUSIVO de tres entradas:

Salida = AB + A•0 + BA + B•0 + 0•A + 0•B

Salida = AB + A•1 + BA + B•1

Salida = AB + A + BA + B

Salida = A(B + 1) + B(A + 1)

Salida = A + B

Poner un "0" lógico permanentemente en cualquiera de las entradas de un OR-EXCLUSIVO lo convierte simplemente en un OR, no en un OR-EXCLUSIVO de dos entradas. Tampoco lo podemos lograr poniendo una de las entradas permanentemente a un "1" lógico, por ejemplo haciendo C=1 en el OR-EXCLUSIVO de tres entradas:

Salida = AB + A•1 + BA + B•1 + 1•A + 1•B

Salida = AB + A•0 + BA + B•0 + A + B

Salida = AB + BA + A + B

Salida = (A + 1)B + (B + 1)A

Salida = A + B

Salida = A · B

Poner un "1" lógico permanentemente en cualquiera de las entradas de un OR-EXCLUSIVO lo convierte simplemente en un NAND, no en un OR-EXCLUSIVO de dos entradas. Sin embargo, lo podemos lograr conectando dos de las entradas en una sola, lo cual equivaldría por ejemplo a hacer C=B en el OR-EXCLUSIVO de tres entradas:

Salida = AB + AC + BA + BC + CA + CB

Salida = AB + AB + BA + BB + BA + BB

Salida = AB + AB + BA + 0 + BA + 0

Salida = AB + AB

Esta es la salida de un OR-EXCLUSIVO de dos entradas. Y esto resuelve el problema.

Habríamos obtenido un resultado similar si hubieramos conectado las entras A y B (haciendo B=A) ó las entradas A y C (haciendo C=A).

PROBLEMA: La Tabla de Verdad para un circuito lógico es la siguiente:

¿Cuál es el diagrama para el circuito de acuerdo con esta Tabla de Verdad? Simplificar el circuito lo más que se pueda.

En este caso, puesto que hay menos ceros que unos, es más conveniente diseñar alrededor de los ceros, o sea usando maxterms. Obtenemos primero de la Tabla de Verdad los maxterms requeridos:

La salida está dada por:

Salida = f₁f₇

Salida = (A + B + C) • (A + B + C)

Simplificando:

Salida = AA + AB + AC + BA + BB + BC + CA + CB + CC

Puesto que AA = 0 y BB = 0, podemos borrar dichos términos y continuar con la simplificación:

Salida = AB + AC + AC + BA + BC + BC + C

Factorizando:

Salida = AB + C(A + A) + BA + C(B + B) + C

Puesto que:

A + A= 1

B + B = 1

La simplificación conduce a:

Salida = AB + C + BA + C + C

Y como C+C = C, la expresión final simplificada será:

Salida = AB + AB + C

El diagrama del circuito correspondiente es como se muestra a continuación: